目录
一、自适应均衡器的仿真流程图:
二、仿真结果:
三、MATLAB仿真代码:
一、自适应均衡器的仿真流程图:
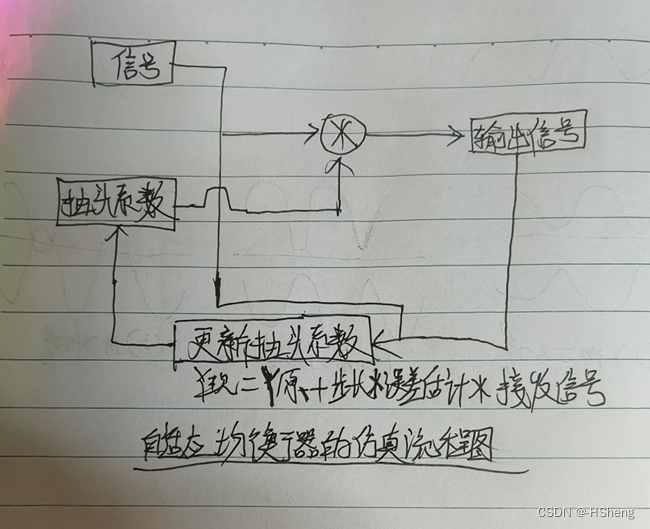
二、仿真结果:
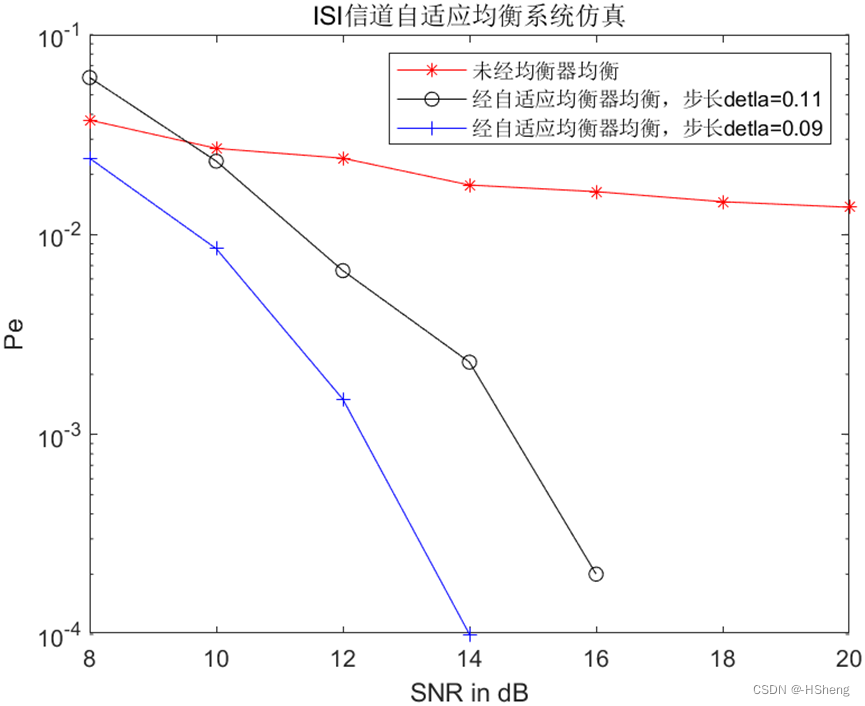
结果分析:
(1)从仿真结果图可以看出,未经过均衡器均衡的码元序列随着SNR的增大,曲线走势情况平缓,变化不大,这表明误码率变化平缓,减小度量最小。总体来看,误码率是曲线图中三者最大的。
(2)从仿真结果图可以看出,在经过均衡器均衡的码元序列中,步长为detla=0.11的码元序列随着SNR的增大,曲线走势呈斜坡下降,变化较大,这表明误码率变化较大,减小度量较大,较三者中居中。总体来看,误码率是曲线图中三者居中的。
(3)从仿真结果图可以看出,在经过均衡器均衡的码元序列中,步长为detla=0.09的码元序列随着SNR的增大,曲线走势也呈斜坡下降,变化大,这表明误码率变化大,减小度量最大,较三者中最大。总体来看,误码率是曲线图中三者最小的。
(4)但是我们还可以从仿真曲线图中看出,当SNR小于等于9时候,经过均衡器均衡并且步长为detla=0.11的码元序列的误码率还大于了未经过均衡器均衡的码元序列的误码率;当SNR小于8时候,经过均衡器均衡并且步长为detla=0.11和detla=0.09的码元序列的误码率均有大于未经过均衡器均衡的码元序列误码率的现象。由此我们可以从本实验得出:当SNR(信道信噪比)小于一定的界限下,使用均衡器均衡的码元序列的误码率不如未经过均衡器均衡的码元序列的误码率低。所以在这里小小推测一下:当SNR(信道信噪比)小于一定的界限下,可以不使用均衡器对码元序列进行均衡。
三、MATLAB仿真代码:
1、MATLAB仿真主函数代码:
clear;
clc;
echo off;
close all;
N=10000; %指定信号序列长度
info=random_binary(N); %产生单极性不归零基带信号序列
input=info*2-1; %单极性码元·变双极性码元
SNR_in_dB=8:2:20; %AWGN信道信噪比 从8到20每一次信噪比加2
for j=1:length(SNR_in_dB)
[y,len]=channel(input,SNR_in_dB(j)); %通过既有码间干扰又有高斯白噪声信道
numoferr=0; %初始误码统计数
for i=len+1:N+len, %从第len个码元开始为真实信号码元
if (y(i)<0), %判决译码
decis=0;
else
decis=1;
end;
if(decis~=info(i-len)), %判断是否误码,统计误码码元个数
numoferr=numoferr+1;
end;
end;
Pe(j)=numoferr/N; %未经均衡器均衡,得到的误码率
end;
figure(1);
semilogy(SNR_in_dB,Pe,'red*-'); %未经均衡器,误码率结果图
hold on; %semilogy表示y坐标轴是对数坐标系
delta_1=0.11; %指定自适应均衡器的步长
delta_2=0.09; %指定自适应均衡器的步长
for j=1:length(SNR_in_dB)
y=channel(input,SNR_in_dB(j)); %通过信道
z=lms_equalizer(y,input,delta_1); %通过自适应均衡器,并设置步长为0.11
numoferr=0;
for i=1:N,
if (z(i)<0),
decis=0;
else
decis=1;
end;
if (decis~=info(i)),
numoferr=numoferr+1;
end;
end;
Pe(j)=numoferr/N; %经自适应均衡器均衡后,得到的误码率
end;
semilogy(SNR_in_dB,Pe,'blacko-'); %自适应均衡器均衡之后,误码率结果图
hold on;
xlabel('SNR in dB');
ylabel('Pe');
title('ISI信道自适应均衡系统仿真');
for j=1:length(SNR_in_dB)
y=channel(input,SNR_in_dB(j)); %通过信道
z=lms_equalizer(y,input,delta_2); %通过自适应均衡器,并设置步长为0.11
numoferr=0;
for i=1:N,
if (z(i)<0),
decis=0;
else
decis=1;
end;
if (decis~=info(i)),
numoferr=numoferr+1;
end;
end;
Pe(j)=numoferr/N; %经自适应均衡器均衡后,得到的误码率
end;
semilogy(SNR_in_dB,Pe,'blue+-'); %自适应均衡器均衡之后,误码率结果图
hold on;
xlabel('SNR in dB');
ylabel('Pe');
title('ISI信道自适应均衡系统仿真');
legend('未经均衡器均衡','经自适应均衡器均衡,步长detla=0.11','经自适应均衡器均衡,步长detla=0.09');
%eyediagram(y(500:1000),10); %均衡前眼图
%eyediagram(z(500:1000),10); %均衡后眼图,步长0.11;
2、仿真脚本函数:random_binary函数
function [ info ] = random_binary( N )
%UNTITLED2 此处显示有关此函数的摘要
% 此处显示详细说明
if nargin == 0, %nargin表示所引用的函数的输入参数的个数
N=10000; %如果没有输入参数,则指定信息序列为10000个码元
end;
for i=1:N,
temp=rand;
if(temp<0.5)
info(i)=0; %1/2的概率
else
info(i)=1;
end
end;
end
3、仿真脚本函数:channel函数
function [ y,len ] = channel( x,snr_in_dB )
%模拟既有码间干扰又有高斯白噪声的信道
SNR=exp(snr_in_dB*log(10)/10); %信噪比真值转换
sigma=1/sqrt(2*SNR); %高斯白噪声的标准差
%指定信道的码间串扰(ISI)参数,可以看出此信道质量还是比较差的
actual_isi=[0.05 -0.063 0.088 -0.126 -0.25 0.9047 0.25 0 0.126 0.038 0.088];
len_actual_isi=(length(actual_isi)-1)/2;
len=len_actual_isi; %len=5
y=conv(actual_isi,x); %信号通过信道,相当于信号序列与信道模型序列作卷积
%需要指出,此时码元序列长度变为N+L=N+2len+1,译码时我们从第len个码元开始到N+len个结束
for i=1:2:size(y,2),
[noise(i) noise(i+1)]=gngauss(sigma); %产生噪声
end;
y=y+noise; %叠加噪声
%也可直接用y = awgn(y,SNR)
end
4、仿真脚本函数:高斯白噪声
function [ gsrv1,gsrv2 ] = gngauss( m,sgma )
%产生高斯白噪声
if nargin ==0, %如果没有输入实参,则均方为0,标准差为1
m=0; sgma=1;
elseif nargin ==1, %如果输入实参为1个参数,则标准差为输入实参,均值为0
sgma=m; m=0;
end
u=rand;
z=sgma*(sqrt(2*log(1/(1-u))));
u=rand;
gsrv1=m+z*cos(2*pi*u);
gsrv2=m+z*sin(2*pi*u);
end
5、仿真脚本函数:抽头
function [ z ] = lms_equalizer( y,info,delta )
%最小均方(LMS)算法自适应滤波器实现 时域均衡器
estimated_c=[0 0 0 0 0 1 0 0 0 0 0]; %初始抽头系数(长度应该是和channel中信道阶数相同=11)
K=5; %K=(length(estimated_c)-1)/2
for k=1:size(y,2)-2*K, %channel中返回参数len的长度也是5,或许K的选择便是基于len,需要K=len
y_k=y(k:k+2*K); %获取码元,一次11个
z_k=estimated_c*y_k'; %各抽头系数与码元相乘后求和
e_k=info(k)-z_k; %误差估计
estimated_c=estimated_c+delta*e_k*y_k;%计算校正抽头系数
z(k)=z_k; %均衡后输出的码元序列
end;
%误差e=d-y,(y指经过信道后的输出信号)这里期望信号d使用的是输入信号info
%比较误码率都是只比较info的长度N
%size(y,2)返回y的列数=N+L-1(L=2len+1),则size(y,2)-2*K=N+L-(2K+1)=N+2(len-K)
%这里将会有个弊端:如果len>K,则k=1:N+2(len-K)会超过info的长度N.
end
猜你喜欢
网友评论
- 搜索
- 最新文章
- 热门文章
