【Verilog编程】线性反馈移位寄存器（LFSR）原理及Verilog代码实现

文章目录

• 一、移位寄存器的基本概念
• • 1.移位寄存器
  • 2.反馈移位寄存器
  • 3.线性反馈移位寄存器
  • • 状态
    • 抽头
    • 种子
    • 二、LFSR的一些基本概念
    • • 1.级数和周期
      • 2.特征多项式
      • 三、LFSR的分类
      • • 1.斐波那契LFSR：多到一型LFSR(many to one)
        • • 从左到右依次递增编号
          • 从右到左依次递减编号
          • 三级斐波那契LFSR的Verilog代码实现
          • 2.伽罗瓦LFSR：一到多型LFSR(one to many)
          • • 从左到右依次递增编号
            • 从左到右依次递减编号
            • 三级伽罗瓦LFSR的Verilog代码实现
            • 3.斐波那契LFSR与伽罗瓦LFSR的对比
            • 4.LFSR的全零禁止态
            • • 斐波那契LFSR禁止态处理
              • • 三级斐波那契LFSR禁止态处理的Verilog代码实现
                • 伽罗瓦LFSR禁止态处理
                • • 三级伽罗瓦LFSR禁止态处理的Verilog代码实现
                  • 参考文献

                    一、移位寄存器的基本概念

                    1.移位寄存器

                    移位寄存器：指若干个寄存器排成一列，每个寄存器中存放1bit二进制数据(0或1)，每个时钟周期向左或向右移动一个bit。下图所示为一个向右移动的移位寄存器。

                    

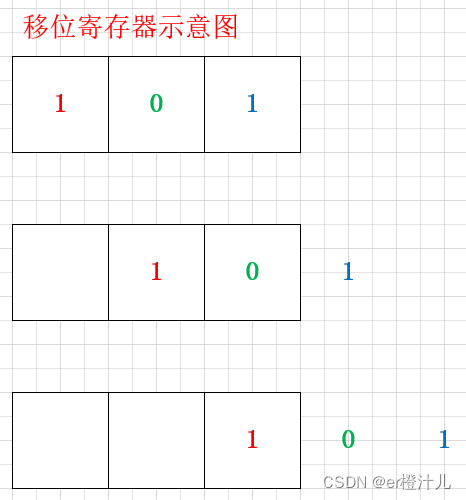
                    2.反馈移位寄存器

                    反馈移位寄存器（Feedback Shift Register，FSR）：每个时钟脉冲，移位寄存器向右移动一位，则移位寄存器的左左侧就会空出一位。这个如果左侧有输入，则移位寄存器的右侧输出端则会有源源不断的数据输出。如果来自移位寄存器的某些序列根据一定的反馈函数形成左侧输入，则称该结构为反馈移位寄存器。

                    

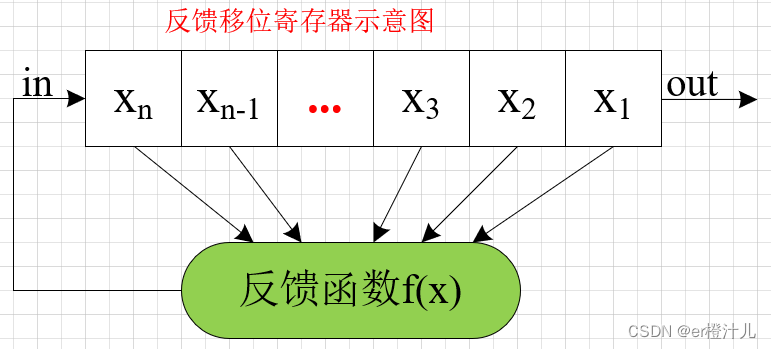
                    3.线性反馈移位寄存器

                    线性反馈移位寄存器（Linear Feedback Shift Register，LFSR）：当反馈移位寄存器的反馈函数f(x)是线性时，则称为线性反馈移位寄存器。

                    

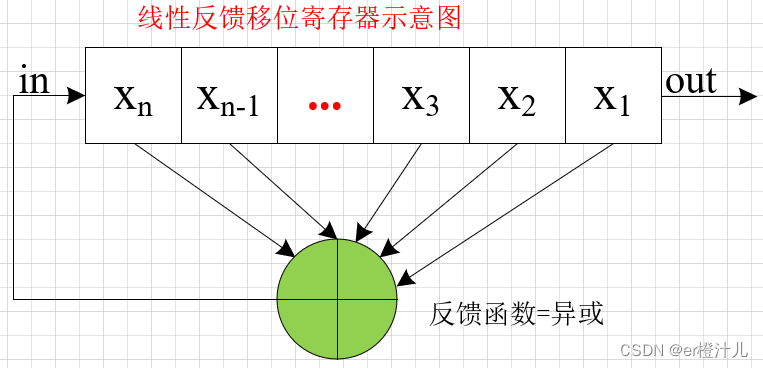
                    线性反馈移位寄存器的反馈函数为：对移位寄存器中的某些位进行异或。将反馈函数得到的计算结果反馈到移位寄存器的最左边，即得到了线性反馈移位寄存器。

                    状态

                    状态：一个LFSR当前存储的序列被称为一个状态。当LFSR向右移动一位时，左侧会被反馈函数补上一位计算后的数据，得到一个新的LFSR序列，此时LFSR就移动到了一个新状态。

                    抽头

                    抽头：线性反馈移位寄存器有些位参与异或，有些位不参与异或，其中参与异或的位被称为抽头。抽头会影响下一状态的比特位。LFSR的触发器编号从1开始，因此抽头的取值范围是1~(2ⁿ-1)。

                    种子

                    种子：LFSR中的初值，种子应该是非零的。如果为全零的话，下一状态任意做异或也还是为0，则线性反馈移位寄存器的输出用于0，无效。

                    二、LFSR的一些基本概念

                    1.级数和周期

                    级数：LFSR中的寄存器个数称为LFSR的级数。一个5级的LFSR最多同时存放5bit数据

                    周期：一个n级的LFSR最多只有(2ⁿ-1)个状态，即：一个n级的LFSR最多只能遍历2ⁿ-1个序列，即最大周期为(2ⁿ-1)。

                    注：nbit移位寄存器能存储的数据为0~(2ⁿ-1),即2ⁿ个状态，但是由于LFSR禁止全0状态，因此一个n级的LFSR最多只能有(2ⁿ-1)个状态。因此一个LFSR的最大周期是(2ⁿ-1)个系统时钟周期，当用LFSR产生PRBS（伪随机噪声）时，是存在周期性的。值得注意的是：不是所有的LFSR都能达到(2ⁿ-1)个周期，这与抽头的设计相关。只要选择合适的反馈函数便可使序列的周期达到最大值(2ⁿ-1)，周期达到最大值的序列称为m序列。

                    2.特征多项式

                    

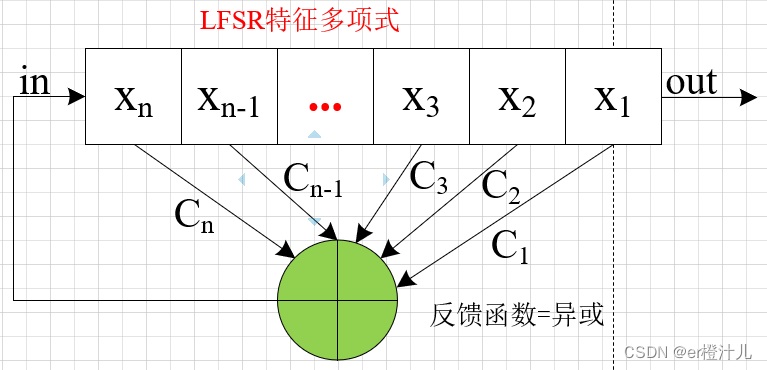
                    由上图，可以得到第n+1位的值为：

                    

                    由上文可以看出，特征多项式表示的是抽头系数，抽头的设计关系到LFSR的最大周期，一般要使LFSR得到最大周期(2^n-1)，可参照如下表：

                    

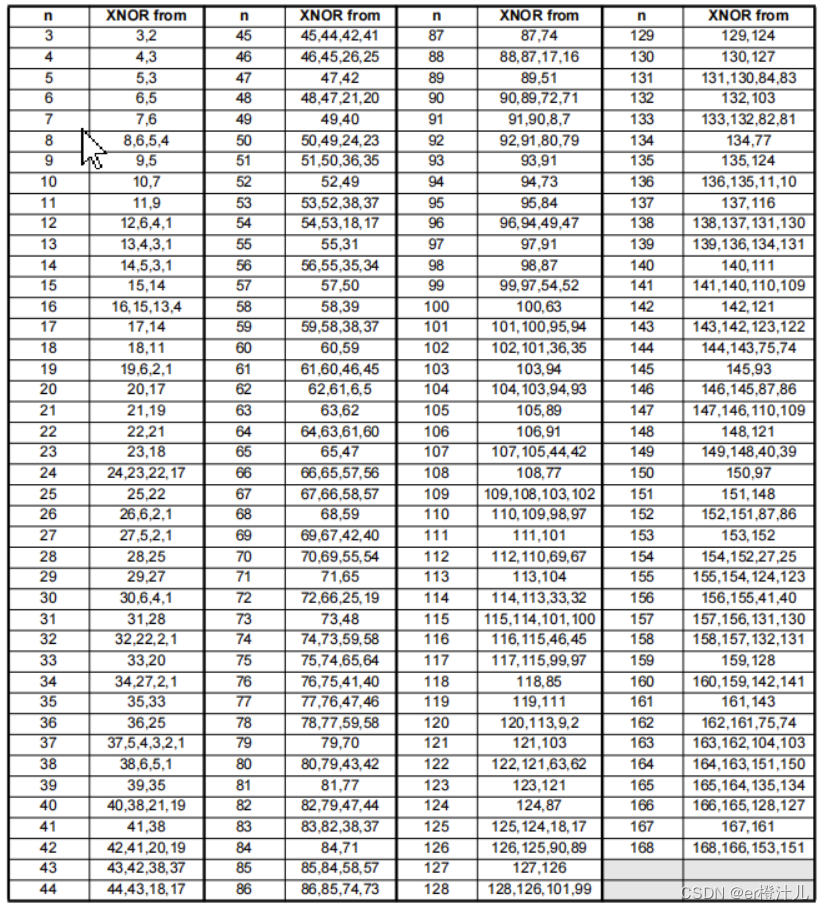
                    三、LFSR的分类

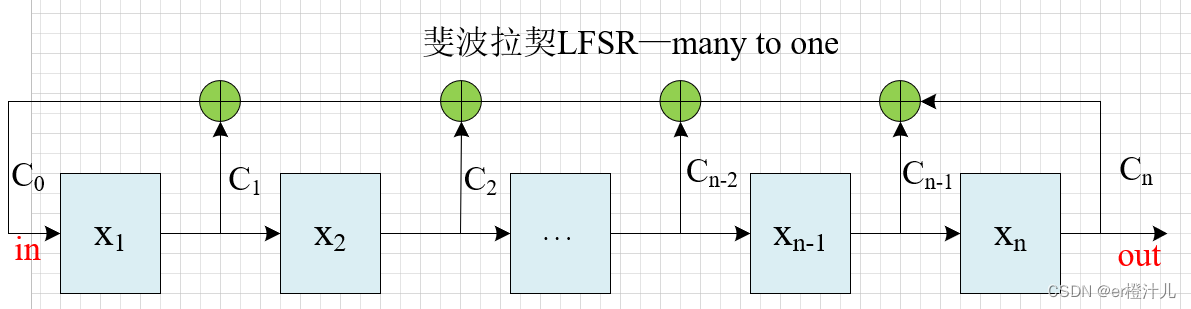
                    1.斐波那契LFSR：多到一型LFSR(many to one)

                    抽头序列对应bit位置的多个寄存器的输出异或后驱动一个寄存器输入

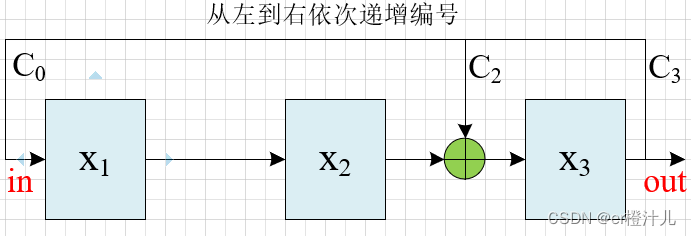
                    从左到右依次递增编号

                    

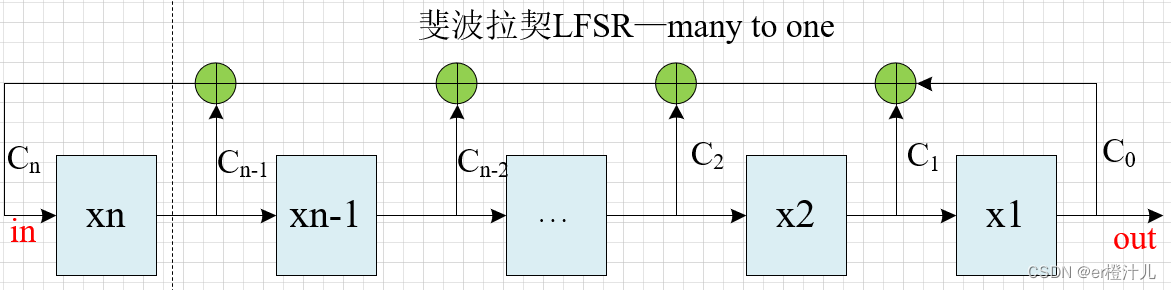
                    从右到左依次递减编号

                    

                    以三级LFSR，反馈函数为：f(x)=x³+x²+1为例，其两种编号的伽罗瓦电路图如下

                    1.从左到右依次递增编号

                    

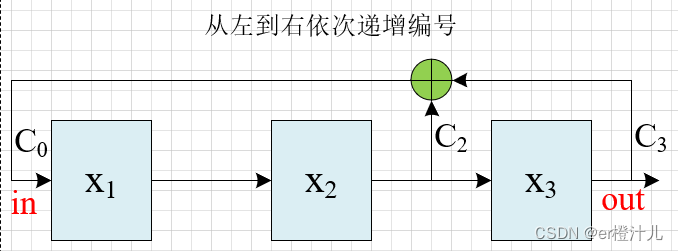
                    假设初始状态为001，则该电路的状态跳转为：

                    

                    周期数为2³-1=7

                    2.从左到右依次递减编号

                    

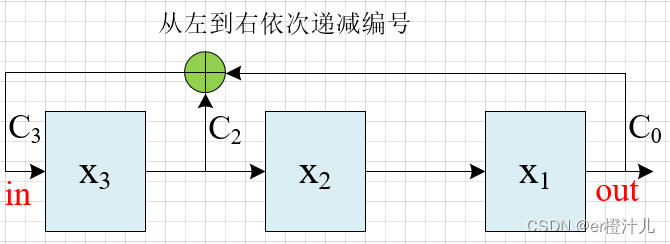
                    假设初始状态为001，则该电路的状态跳转为：

                    

                    周期数为2³-1=7

                    斐波那契LFSR习惯采用“从左到右依次递增编号”的电路。

                    三级斐波那契LFSR的Verilog代码实现

                    `timescale	1ns/1ps
                    module fibonacci_lfsr(
                    	input		wire						sclk,
                    	input		wire						rst_n,
                    	output		reg 						flfsrn
                    );
                    reg	[1:3]	fibo_lfsr;//f(x)=x^3+x^2+1，从左到右依次递增编号
                    always	@(posedge	sclk or negedge	rst_n)begin
                    	if(rst_n==1'b0)begin
                    		fibo_lfsr<=3'b001;//initial value
                    	end
                    	else	begin
                    		fibo_lfsr<={fibo_lfsr[3]^fibo_lfsr[2],fibo_lfsr[1],fibo_lfsr[2]};
                    	end
                    end
                    always	@(*)begin
                    	flfsrn=fibo_lfsr[3];
                    end
                    endmodule
                    

                    仿真图如下所示，符合预期状态转移过程。

                    

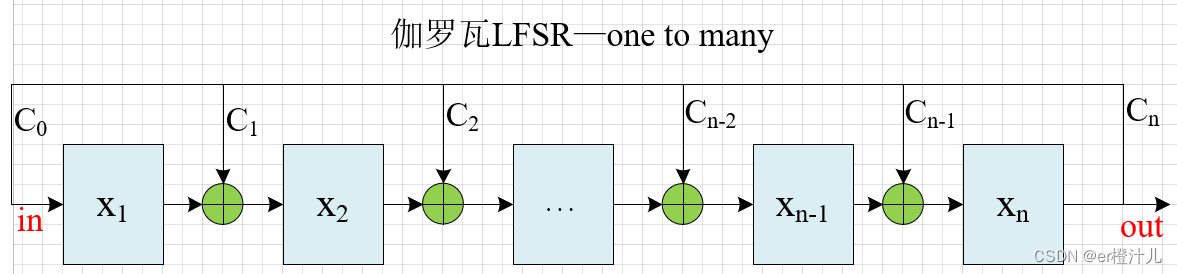
                    2.伽罗瓦LFSR：一到多型LFSR(one to many)

                    最后一个寄存器的输出通过与抽头序列对应位置寄存器前一级寄存器的输出异或后驱动多个抽头序列对应位置的寄存器

                    从左到右依次递增编号

                    

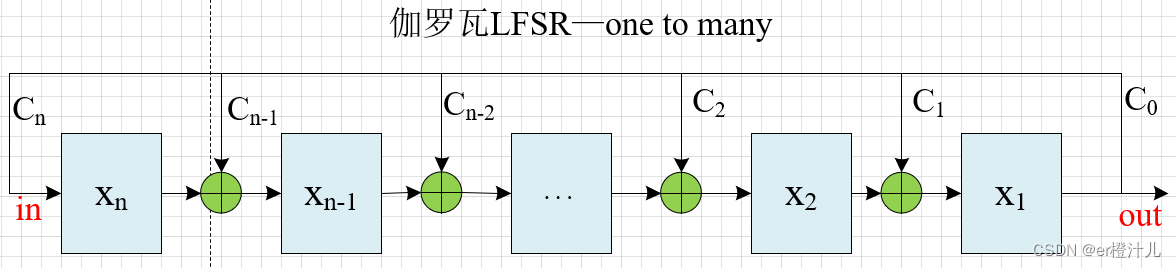
                    从左到右依次递减编号

                    

                    以三级LFSR，反馈函数为：f(x)=x³+x²+1为例，其两种编号的伽罗瓦电路图如下

                    1.从左到右依次递增编号

                    

                    假设电路初始值为001，则该电路的状态跳转为：

                    

                    周期数为2³-1=7

                    2.从左到右依次递减编号

                    

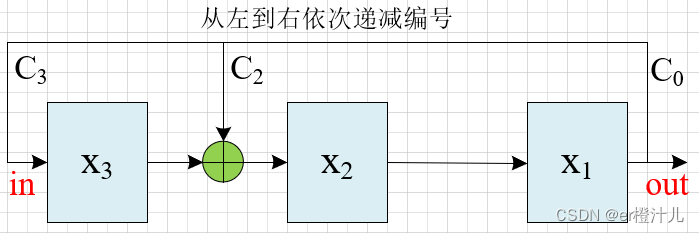
                    假设电路初始值为001，则该电路的状态跳转为：

                    

                    周期数为2³-1=7

                    伽罗瓦LFSR习惯采用“从左到右依次递减编号”电路。

                    三级伽罗瓦LFSR的Verilog代码实现

                    `timescale	1ns/1ps
                    module galois_lfsr(
                    	input		wire						sclk,
                    	input		wire						rst_n,
                    	output		reg							glfsrn
                    );
                    reg	[3:1]	galo_lfsr;//f(x)=x^3+x^2+1,从左到右依次递减编号
                    always	@(posedge	sclk or negedge	rst_n)begin
                    	if(rst_n==1'b0)begin
                    		galo_lfsr<=3'b000;//initial value
                    	end
                    	else begin
                    		galo_lfsr<={galo_lfsr[1],galo_lfsr[3]^galo_lfsr[1],galo_lfsr[2]};
                    	end
                    end
                    always	@(*)begin
                    	glfsrn=galo_lfsr[1];
                    end
                    endmodul
                    

                    仿真图如下所示，符合预期状态转移过程。

                    

                    3.斐波那契LFSR与伽罗瓦LFSR的对比

                    伽罗瓦LFSR具有更高的速度，因为两个触发器之间只有一个异或门。斐波那契LFSR在首尾两个寄存器之间有多个异或门，组合逻辑延时更大，因为为了满足建立保持时间的要求，其频率更小（周期更大），速度更慢。

                    4.LFSR的全零禁止态

                    由上文的分析，当LFSR的某个状态为全0后，无论怎么组合，0与0异或都为0，因此LFSR将一直输出0，得不到想要的序列，因此LFSR要避免进入全零状态。其预防的办法有：

                    （1）将寄存器置位到某个允许的状态

                    if(|lfsr[n-1:0]==1'b0)begin
                    			lfsr[n-1:0]<={{n}{1'b1}};//如果为全零状态，则下一个状态置为全1。
                    		end
                    

                    （2）使用额外的电路使得电路进入全零状态后自动退出

                    斐波那契LFSR禁止态处理

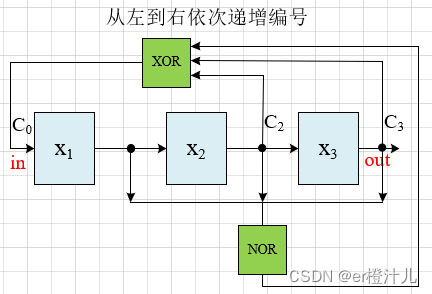
                    如对于斐波那契LFSR，额外添加一个n位或非（NOR）逻辑，如下电路图

                    

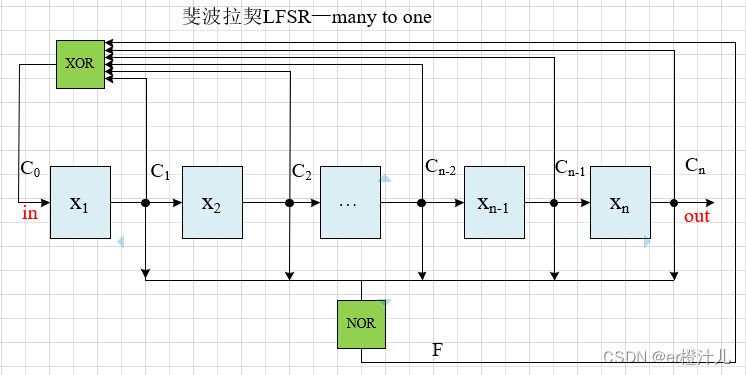
                    (1)当LFSR为全零时，F=1，那么LFSR的状态跳变为：00…00—>00…01,LFSR从全零状态退出

                    (2)当LFSR不为全零时，F=0，此时

                    

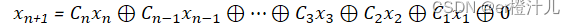
                    由于任何数（0或1）异或0都等于其本身，因此

                    

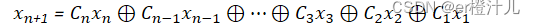
                    故当LFSR不为全零时，不会对电路造成影响。

                    如对一个三级LFSR，特征多项式为f(x)=x³+x²+1，"从左到右依次递增编号"的斐波那契LFSR，加上“保险”后的电路为：

                    

                    三级斐波那契LFSR禁止态处理的Verilog代码实现

                    `timescale	1ns/1ps
                    module fibonacci_lfsr(
                    	input		wire						sclk,
                    	input		wire						rst_n,
                    	output		reg 						flfsrn
                    );
                    reg	[1:3]	fibo_lfsr;//f(x)=x^3+x^2+1,从左到右依次递增编号
                    wire		all_lfsr_not_0;
                    assign	all_lfsr_not_0=~(fibo_lfsr!=3'b000);
                    always	@(posedge	sclk or negedge	rst_n)begin
                    	if(rst_n==1'b0)begin
                    		fibo_lfsr<=3'b001;//initial value
                    	end
                    	else	begin
                    		fibo_lfsr<={fibo_lfsr[3]^fibo_lfsr[2]^all_lfsr_not_0,fibo_lfsr[1],fibo_lfsr[2]};
                    	end
                    end
                    always	@(*)begin
                    	flfsrn=fibo_lfsr[3];
                    end
                    endmodule
                    

                    仿真图如下，当LFSR从全0状态启动后，LFSR自动进入下一状态，符合预期。

                    

                    伽罗瓦LFSR禁止态处理

                    同理对伽罗瓦LFSR添加一个n位或非（NOR）逻辑，如下电路图

                    

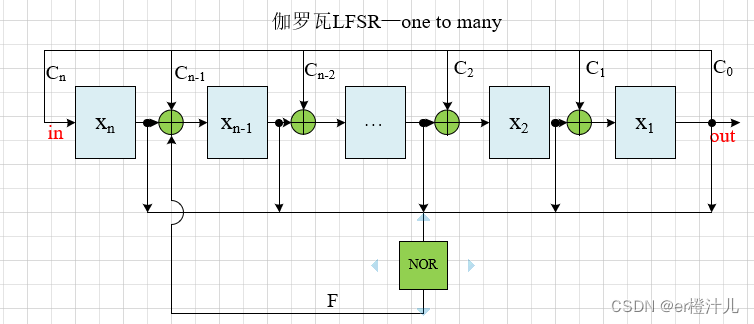
                    （1）当LFSR为全零时，F=1，那么LFSR的状态跳变为：00…00—>01…00,LFSR从全零状态退出

                    （2）当LFSR不为全零时，F=0，此时

                    

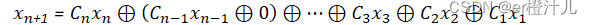
                    由于任何数（0或1）异或0都等于其本身，因此

                    

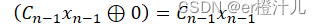
                    故

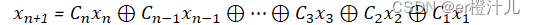
                    故当LFSR不为全零时，不会对电路造成影响。

                    如对一个三级LFSR，特征多项式为f(x)=x³+x²+1，"从左到右依次递减编号"的伽罗瓦LFSR，加上“保险”后的电路为：

                    

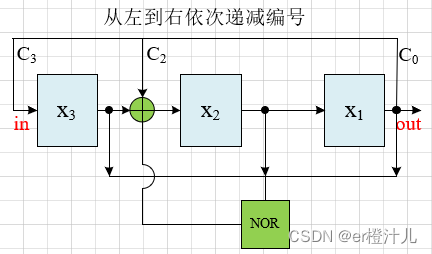
                    三级伽罗瓦LFSR禁止态处理的Verilog代码实现

                    `timescale	1ns/1ps
                    module galois_lfsr(
                    	input		wire						sclk,
                    	input		wire						rst_n,
                    	output		reg							glfsrn
                    );
                    reg	[3:1]	galo_lfsr;//f(x)=x^3+x^2+1,从左到右依次递减编号
                    wire		all_lfsr_not_0;
                    assign	all_lfsr_not_0=~(galo_lfsr!=3'b000);
                    always	@(posedge	sclk or negedge	rst_n)begin
                    	if(rst_n==1'b0)begin
                    		galo_lfsr<=3'b000;//initial value
                    	end
                    	else begin
                    		galo_lfsr<={galo_lfsr[1],galo_lfsr[3]^galo_lfsr[1]^all_lfsr_not_0,galo_lfsr[2]};
                    	end
                    end
                    always	@(*)begin
                    	glfsrn=galo_lfsr[1];
                    end
                    endmodul
                    

                    仿真图如下，当LFSR从全0状态启动后，LFSR自动进入下一状态，符合预期。

                    

                    参考文献

                    1.详解线性反馈移位寄存器（LFSR）

                    2.LFSR(线性反馈移位寄存器)

                    3.线性反馈移位寄存器（LFSR）