
个人主页:日刷百题
系列专栏:〖C/C++小游戏〗〖Linux〗〖数据结构〗 〖C语言〗
🌎欢迎各位→点赞👍+收藏⭐️+留言📝

前言:
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。 基本思想:任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
递归实现方式常见有三种,区别于单趟思想,性能差别不大,下面我们看下快排递归实现。
一、快速排序的递归实现
1.1 Hoare排序
1.1.1 单趟目的
左子序列中所有元素均小于基准值key,右子序列中所有元素均大于基准值key。
1.1.2 动图解析
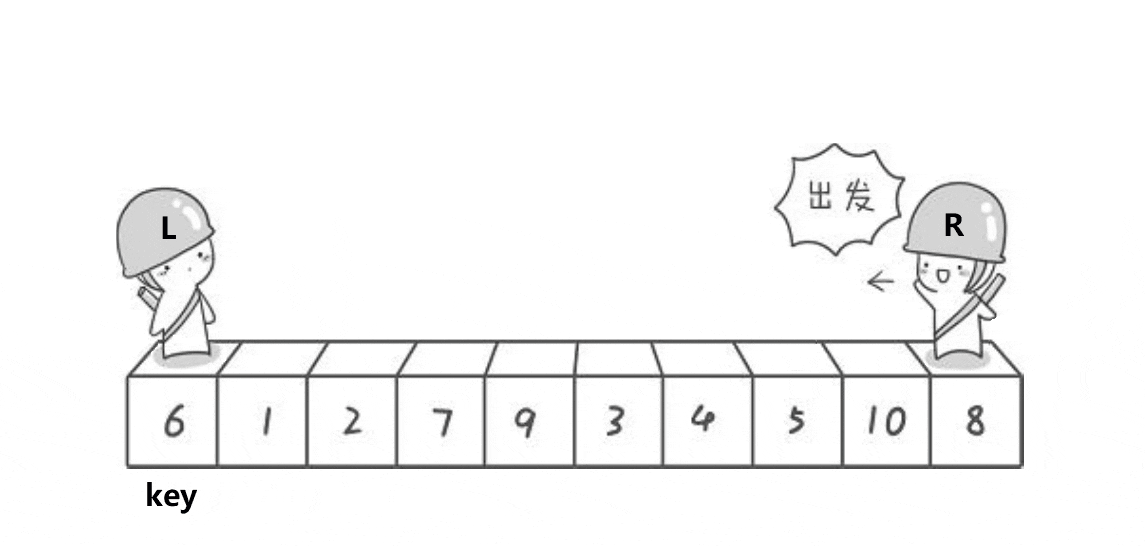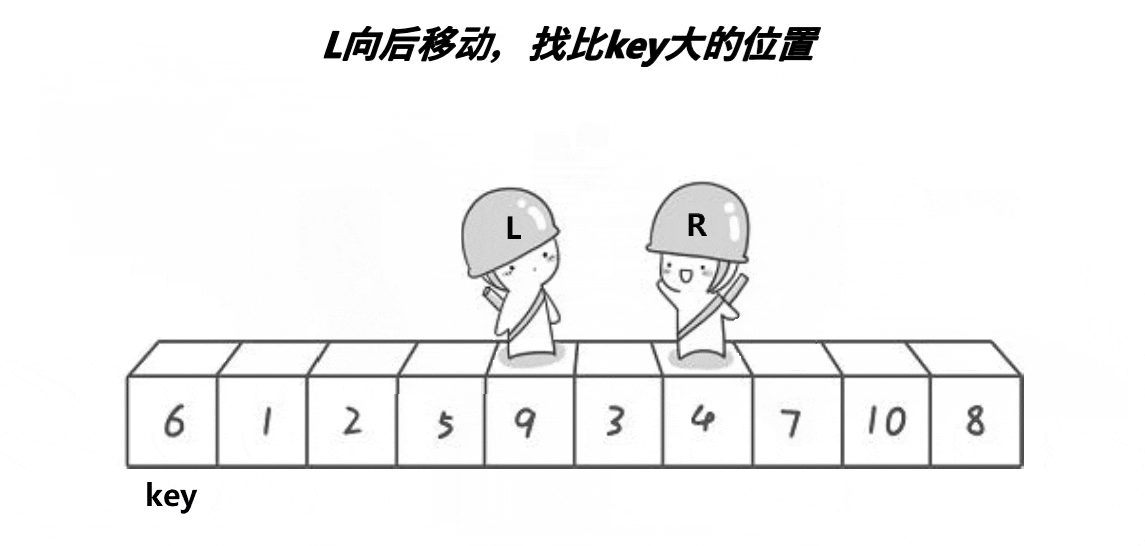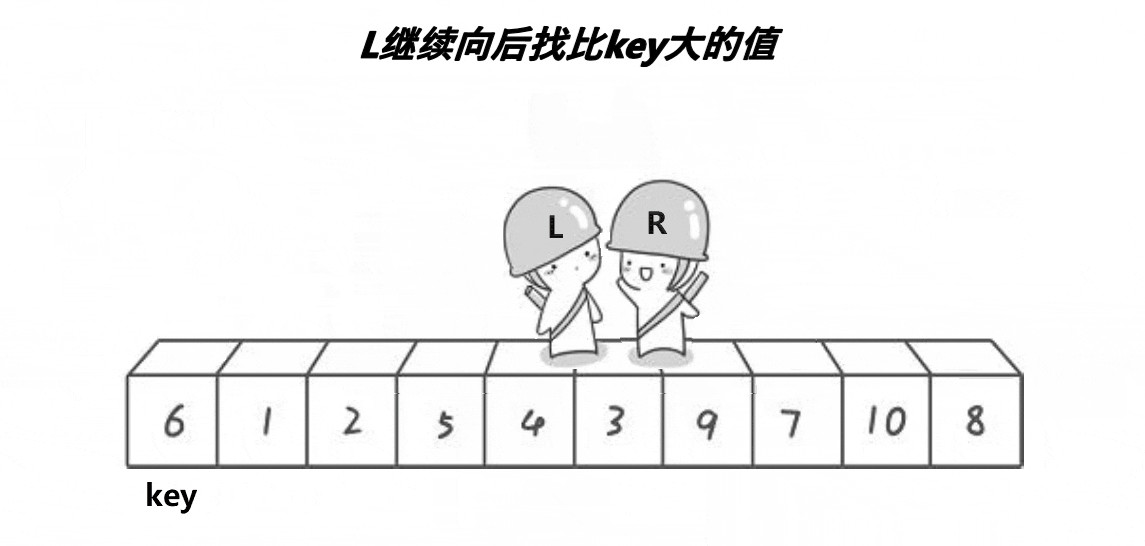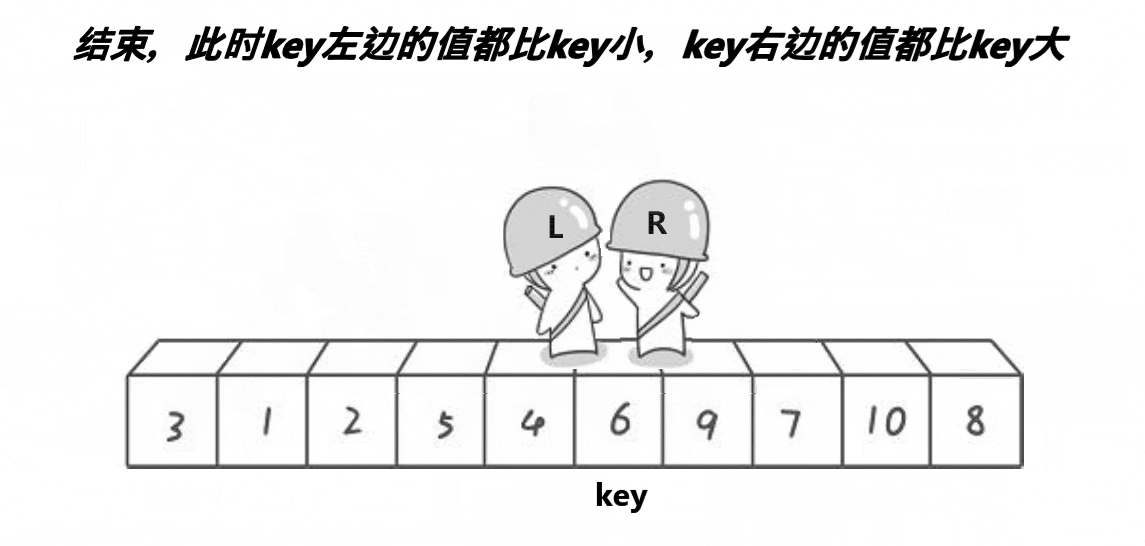
单趟思路:
(1)首先记录下keyi位置为最左边位置,然后left和right分别从数组两端开始往中间走。
(2)right先开始向中间行动,如果right处的值小于keyi处的值,则停止等待left走。
(3)left开始行动,当left找到比keyi处小的值时,left和right处的值进行交换。
(4)当两个位置相遇时,将相遇位置的值与keyi处的值进行交换。
该排序有一个需要注意的点是:必须左边先走找小
因为左边先走,必定相遇时位置对应的值小于keyi位置值,保证最后这俩个位置交换,相遇位置即是keyi位置对应值最终位置。
解析:
(1)右边先走,假设left遇到right,最后相遇情况是right找到了小于keyi位置的值,left没有找到大于keyi位置值,所以相遇位置值小于keyi位置值。
(2)右边先走,假设right遇到left,最后相遇情况是left找到大,right找到小,left与right互换,left位置对应值小于keyi位置值,right继续找小,与left相遇,所以相遇位置值小于keyi位置值。
1.1.3 代码实现
解析:
该代码将单趟写在子函数中,这样使得整个代码层次更加清晰,也便于理解。可以发现我们对单趟中keyi做了优化,因为keyi的位置,是影响快速排序效率的重大因素。因此我们采用了三数取中的方法解决选keyi不合适的问题。即知道这组无序数列的首和尾后,我们只需要在首,中,尾这三个数据中,选择一个排在中间的数据作为基准值(keyi),进行快速排序,即可进一步提高快速排序的效率。
后面2种单趟也做这样的优化,后面就不过多介绍。
//Hoare快排
int GetMid(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[end] > a[mid])
{
return end;
}
else
{
if (a[begin] > a[mid])
{
return mid;
}
else
{
return begin;
}
}
}
else//(a[begin]<= a[end])
{
if (a[begin] > a[mid])
{
return begin;
}
else
{
if (a[end] > a[mid])
{
return mid;
}
else
{
return end;
}
}
}
}
void swap(int* x, int* y)
{
int z = *x;
*x = *y;
*y = z;
}
int _QuickSort_Hoare(int* a, int begin, int end)
{
int mid = GetMid(a,begin, end);
swap(&a[begin], &a[mid]);
int keyi = begin;
int left = begin;
int right = end;
while (left < right)
{
//右边找小
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边找大
while (left < right && a[left] <= a[keyi])
{
left++;
}
swap(&a[left], &a[right]);
}
swap(&a[keyi], &a[left]);
return left;
}
void QuickSort_Hoare(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi= _QuickSort_Hoare(a, begin, end);//单趟
//递归 [begin,keyi-1] keyi,[keyi+1,end]
QuickSort_Hoare(a, begin, keyi - 1);
QuickSort_Hoare(a, keyi+1, end);
}
1.2 挖坑法
1.2.1 单趟目的
左子序列中所有元素均小于基准值key,右子序列中所有元素均大于基准值key。
1.2.2 动图解析
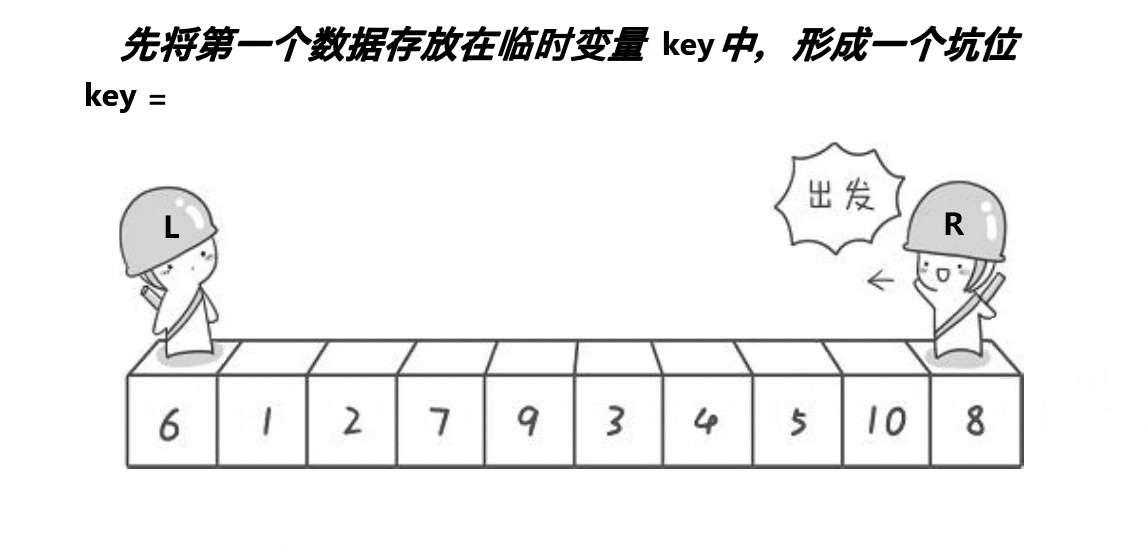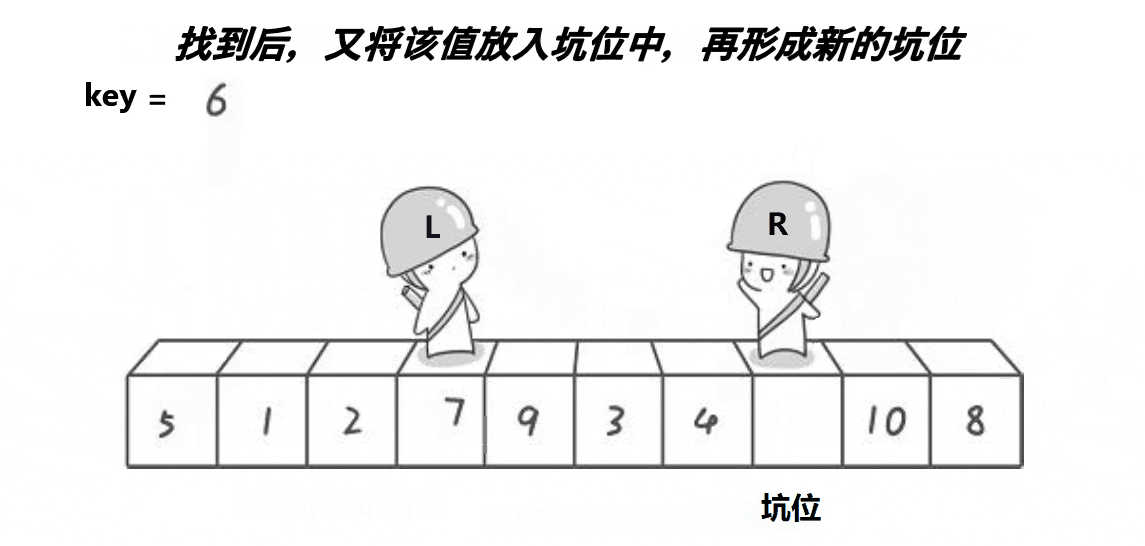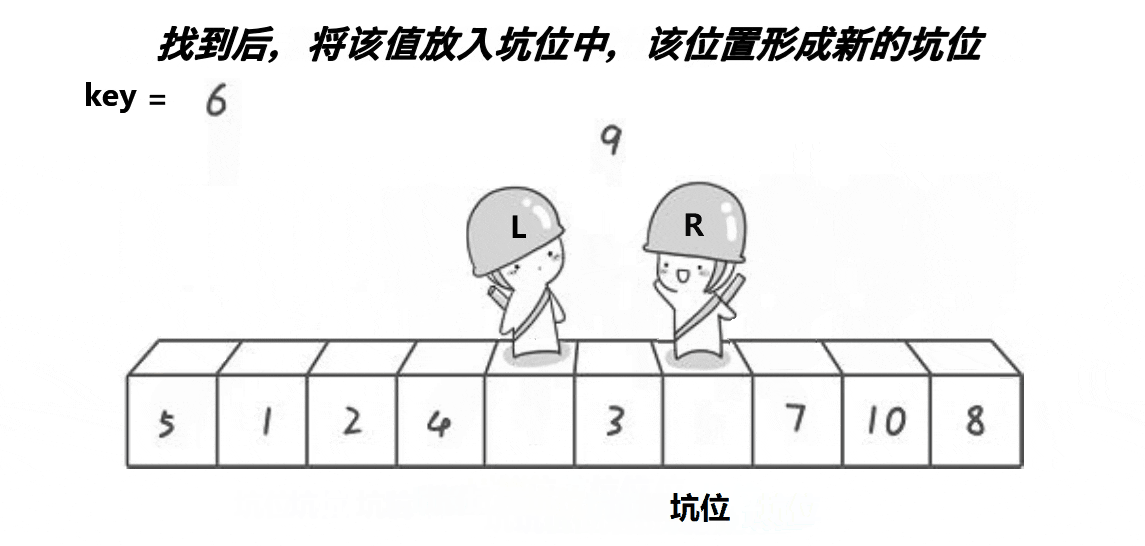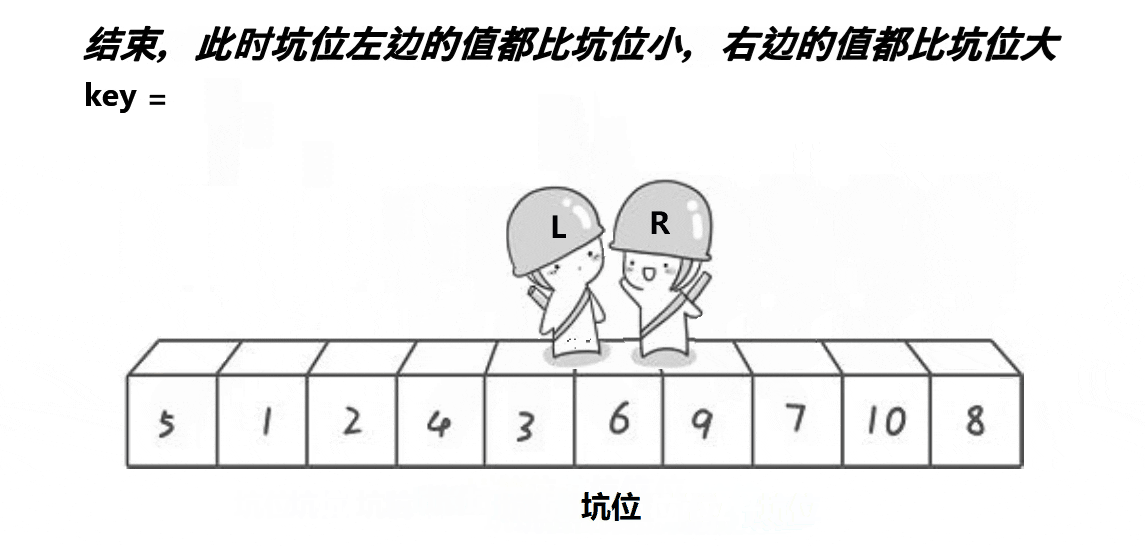
单趟思路:
(1)将begin处的值放到key中,将其置为坑位(pit)
(2)right找到比key小的值后将值放入坑位,然后将此处置为新的坑。
(3) left找到比key大的值后将值放入坑位,然后将此处置为新的坑。
(4)当left与right相遇的时候,将key放入到坑位中。
1.2.3 代码实现
int GetMid(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[end] > a[mid])
{
return end;
}
else
{
if (a[begin] > a[mid])
{
return mid;
}
else
{
return begin;
}
}
}
else//(a[begin]<= a[end])
{
if (a[begin] > a[mid])
{
return begin;
}
else
{
if (a[end] > a[mid])
{
return mid;
}
else
{
return end;
}
}
}
}
void swap(int* x, int* y)
{
int z = *x;
*x = *y;
*y = z;
}
int _QuickSort_Pit(int* a, int begin, int end)
{
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int pit = begin;
int key = a[begin];
int left = begin;
int right = end;
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[pit] = a[right];
pit = right;
while(left < right&& a[left] <= key)
{
left++;
}
a[pit] = a[left];
pit = left;
}
a[left] = key;
return left;
}
void QuickSort_Pit(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = _QuickSort_Pit(a, begin, end);
//[begin,keyi-1],keyi,[keyi+1,end]
QuickSort_Pit(a, begin, keyi - 1);
QuickSort_Pit(a, keyi + 1, end);
}
1.3 双指针法
1.3.1 单趟目的
左子序列中所有元素均小于基准值key,右子序列中所有元素均大于基准值key。
1.3.2 动图解析
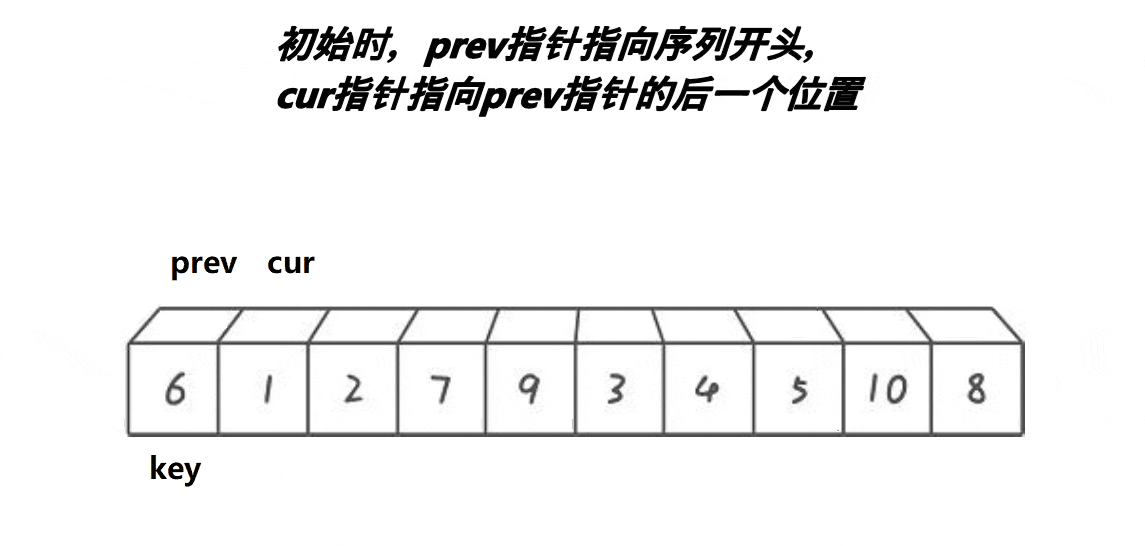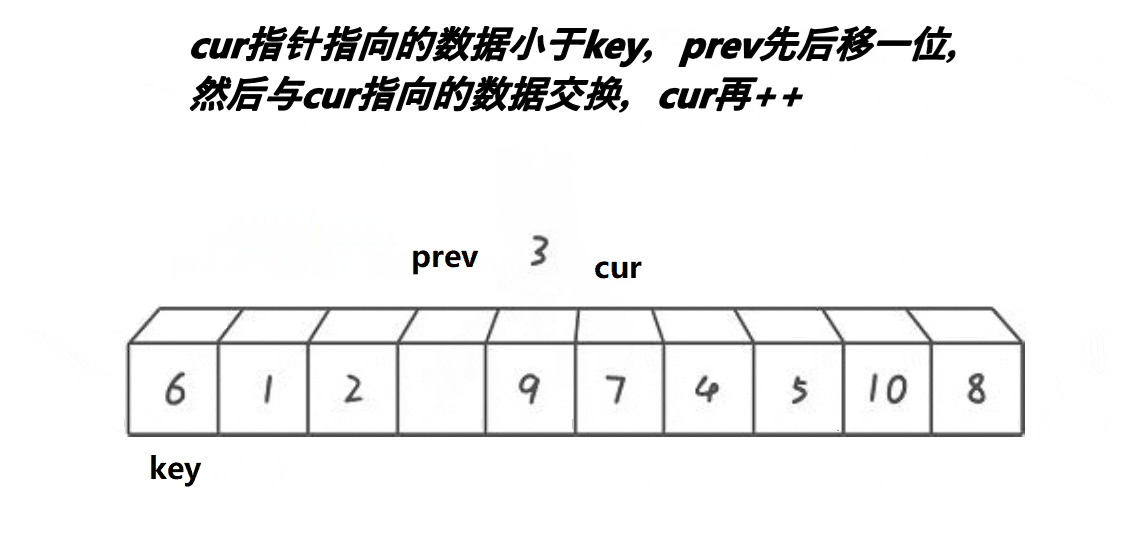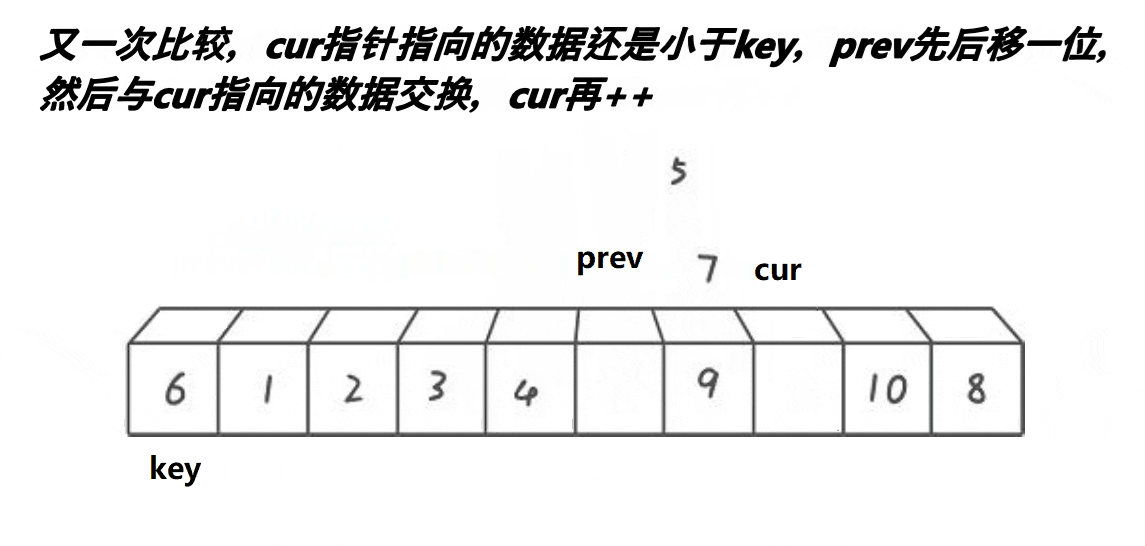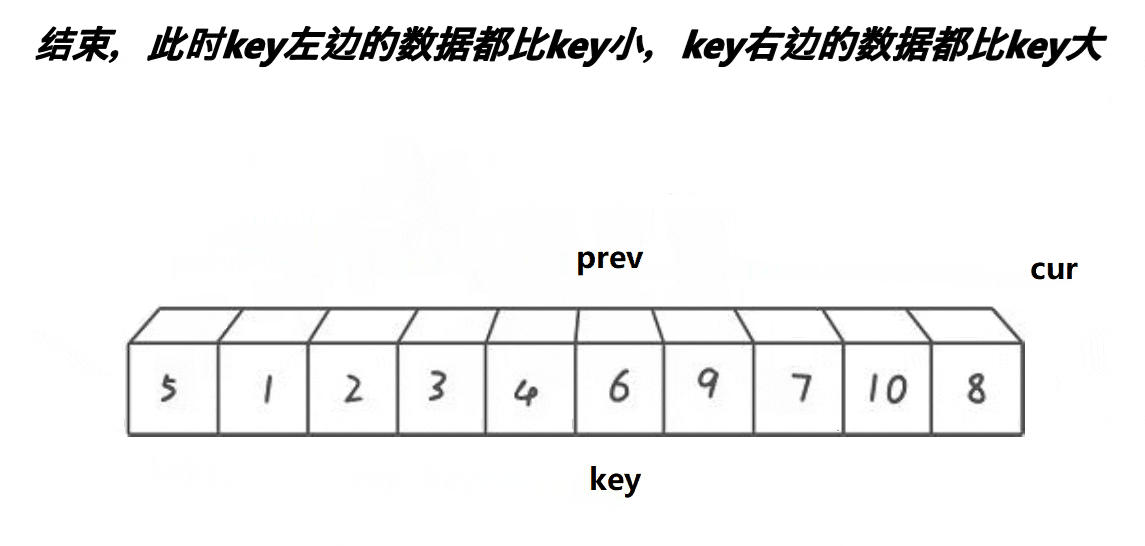
单趟思路:
(1)cur位于begin+1的位置,prev位于begin位置,keyi先存放begin处的值。
(2)如果cur处的值大于key处的值,cur++.
(3)如果cur处的值小于等于key处的值,cur处的值,则与prev+1处的值进行交换。
(4)当循环结束时,将prev处的值与keyi的值相交换,返回prev
1.3.3 代码实现
int GetMid(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[end] > a[mid])
{
return end;
}
else
{
if (a[begin] > a[mid])
{
return mid;
}
else
{
return begin;
}
}
}
else//(a[begin]<= a[end])
{
if (a[begin] > a[mid])
{
return begin;
}
else
{
if (a[end] > a[mid])
{
return mid;
}
else
{
return end;
}
}
}
}
void swap(int* x, int* y)
{
int z = *x;
*x = *y;
*y = z;
}
int _QuickSort_Pointer(int* a, int begin, int end)
{
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int key = begin;
int prev= begin;
int cur = prev + 1;
while (cur <= end)
{
if (a[cur] > a[key])
{
cur++;
}
else
{
prev++;
swap(&a[prev], &a[cur]);
cur++;
}
}
swap(&a[key], &a[prev]);
return prev;
}
void QuickSort_Pointer(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int keyi = _QuickSort_Pointer(a, begin, end);
//[begin,keyi-1],keyi,[keyi+1,end]
QuickSort_Pointer(a, begin, keyi - 1);
QuickSort_Pointer(a, keyi + 1, end);
}
二、快速排序的优化
2.1 三数取中法选key
这个方法提升效率比较显著,上面已经排序均用该方法优化。
2.2 递归到小的子区间,使用插入排序
由于快速排序是递归进行的,当递归到最后三层时,此时数组中的值其实已经接近有序,而且这段区间再递归会极大占用栈(函数栈帧开辟的地方)的空间,最后三层的递归次数占总递归次数的百分之90,所以在区间数据量小于10,我们就不进行递归快速排序了,转而使用插入排序。
int GetMid(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[end] > a[mid])
{
return end;
}
else
{
if (a[begin] > a[mid])
{
return mid;
}
else
{
return begin;
}
}
}
else//(a[begin]<= a[end])
{
if (a[begin] > a[mid])
{
return begin;
}
else
{
if (a[end] > a[mid])
{
return mid;
}
else
{
return end;
}
}
}
}
void swap(int* x, int* y)
{
int z = *x;
*x = *y;
*y = z;
}
int _QuickSort_Pointer(int* a, int begin, int end)
{
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int key = begin;
int prev= begin;
int cur = prev + 1;
while (cur <= end)
{
if (a[cur] > a[key])
{
cur++;
}
else
{
prev++;
swap(&a[prev], &a[cur]);
cur++;
}
}
swap(&a[key], &a[prev]);
return prev;
}
void QuickSort_Pointer(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if(end-begin+1>10)
{
int keyi = _QuickSort_Pointer(a, begin, end);
//[begin,keyi-1],keyi,[keyi+1,end]
QuickSort_Pointer(a, begin, keyi - 1);
QuickSort_Pointer(a, keyi + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
三、快速排序的非递归实现
递归改为非递归,一般2种方法:
1、递归转化为非递归可以写成循环,比如斐波那契数列
2、递归转化为非递归可以写成栈,比如现在的快排
递归使用的空间是栈空间,所以容易出现栈溢出的情况,我们将快速排序改为非递归版本,这样空间的开辟就在堆上了,这样也就解决了这个问题。
快速排序的非递归与递归思想相同,非递归使用栈来模拟递归的实现,思路如下:
(1)入栈一定要保证先入左再入右。
(2)取出两次栈顶的元素,然后进行单趟排序
(3)将区间分为[left , keyi - 1] ,keyi ,[ keyi + 1 , right ] 进行右、左入栈。若区间不存在或为1个值则不入栈。
(4)循环2、3步骤直到栈为空。
代码实现:
int GetMid(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] > a[end])
{
if (a[end] > a[mid])
{
return end;
}
else
{
if (a[begin] > a[mid])
{
return mid;
}
else
{
return begin;
}
}
}
else//(a[begin]<= a[end])
{
if (a[begin] > a[mid])
{
return begin;
}
else
{
if (a[end] > a[mid])
{
return mid;
}
else
{
return end;
}
}
}
}
void swap(int* x, int* y)
{
int z = *x;
*x = *y;
*y = z;
}
int _QuickSort_Pointer(int* a, int begin, int end)
{
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int key = begin;
int prev= begin;
int cur = prev + 1;
while (cur <= end)
{
if (a[cur] > a[key])
{
cur++;
}
else
{
prev++;
swap(&a[prev], &a[cur]);
cur++;
}
}
swap(&a[key], &a[prev]);
return prev;
}
typedef int DateType;
typedef struct Stack
{
DateType* a;
int top;
int capacity;
}Stack;
//初始化和销毁栈
void InitStack(Stack* ps)
{
assert(ps);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
void DestoryStack(Stack* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
//出栈和入栈
void StackPush(Stack* ps, DateType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
DateType* tmp = (DateType*)realloc(ps->a, sizeof(DateType) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail:");
return;
}
ps->a = tmp;
ps->capacity = newcapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
//栈的有效个数和栈顶元素
int StackSize(Stack* ps)
{
assert(ps);
return ps->top;
}
DateType StackTop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
//判空
bool IsEmptyStack(Stack* ps)
{
assert(ps);
return ps->top == 0;
}
void QuickSort_Non_r(int* a, int begin, int end)
{
Stack tmp;
InitStack(&tmp);
StackPush(&tmp,end);
StackPush(&tmp, begin);
while (!IsEmptyStack(&tmp))
{
int left = StackTop(&tmp);
StackPop(&tmp);
int right = StackTop(&tmp);
StackPop(&tmp);
int keyi = _QuickSort_Pointer(a, left, right);
if (keyi+1
总结:本篇文章总结了快速排序的递归及非递归俩大种方式。
希望大家阅读完可以有所收获,同时也感谢各位铁汁们的支持。文章有任何问题可以在评论区留言,百题一定会认真阅读!
猜你喜欢
网友评论
- 搜索
- 最新文章
- 热门文章
