数据结构第十三弹---链式二叉树基本操作(上)

链式二叉树

• 1、结构定义
• 2、手动创建二叉树
• 3、前序遍历
• 4、中序遍历
• 5、后序遍历
• 6、层序遍历
• 7、计算结点个数
• 8、计算叶子结点个数
• 9、计算第K层结点个数
• 10、计算树的最大深度
• 总结

  1、结构定义

  实现一个数据结构少不了数据的定义，所以第一步需要定义二叉树的机构。

  typedef char BTDataType;//定义数据类型，可以根据需要更改
  typedef struct BinaryTreeNode
  {
  	struct BinaryTreeNode* left;//左指针
  	struct BinaryTreeNode* right;//右指针
  	BTDataType data;//存储数据
  }BTNode;
  

  2、手动创建二叉树

  初次学习链式二叉树，对于创建一个二叉树较难理解，所以先手动创建二叉树，学习一些操作之后再来通过函数实现链式二叉树。

  //创建结点函数
  BTNode* BuyTree(BTDataType x)
  {
  	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
  	newnode->data = x;
  	newnode->left = NULL;
  	newnode->right = NULL;
  	return newnode;
  }
  //创建结点
  	BTNode* A = BuyTree('A');
  	BTNode* B = BuyTree('B');
  	BTNode* C = BuyTree('C');
  	BTNode* D = BuyTree('D');
  	BTNode* E = BuyTree('E');
  	BTNode* F = BuyTree('F');
  //链接结点
  	A->left = B;
  	A->right = E;
  	B->left = C;
  	B->right = D;
  	E->left = F;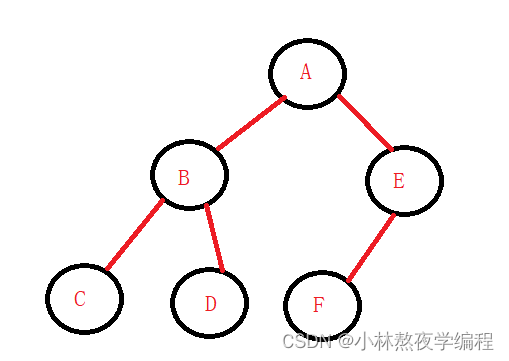
  

  

  3、前序遍历

  前序遍历，又称先根遍历。

  遍历顺序：根，左子树，右子树。

  代码实现

  void PrevOrder(BTNode* root)
  {
  	if (root == NULL)
  	{
  		printf("NULL ");
  		return;
  	}
  	printf("%c ", root->data);//根
  	PrevOrder(root->left);//左子树
  	PrevOrder(root->right);//右子树
  }
  

  此处实现的遍历版本是将空指针也打印出来的版本，更适合新手理解

  测试

  

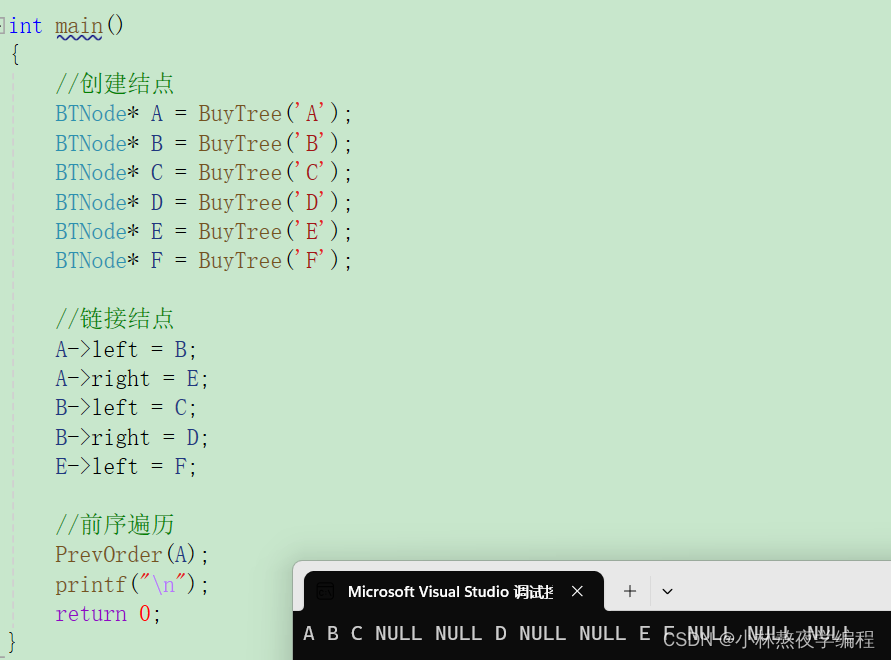
  4、中序遍历

  中序遍历，又称中根遍历。

  遍历顺序：左子树，根，右子树。

  代码实现

  void InOrder(BTNode* root)
  {
  	if (root == NULL)
  	{
  		printf("NULL ");
  		return;
  	}
  	InOrder(root->left);//左子树
  	printf("%c ", root->data);//根
  	InOrder(root->right);//右子树
  }
  

  测试

  

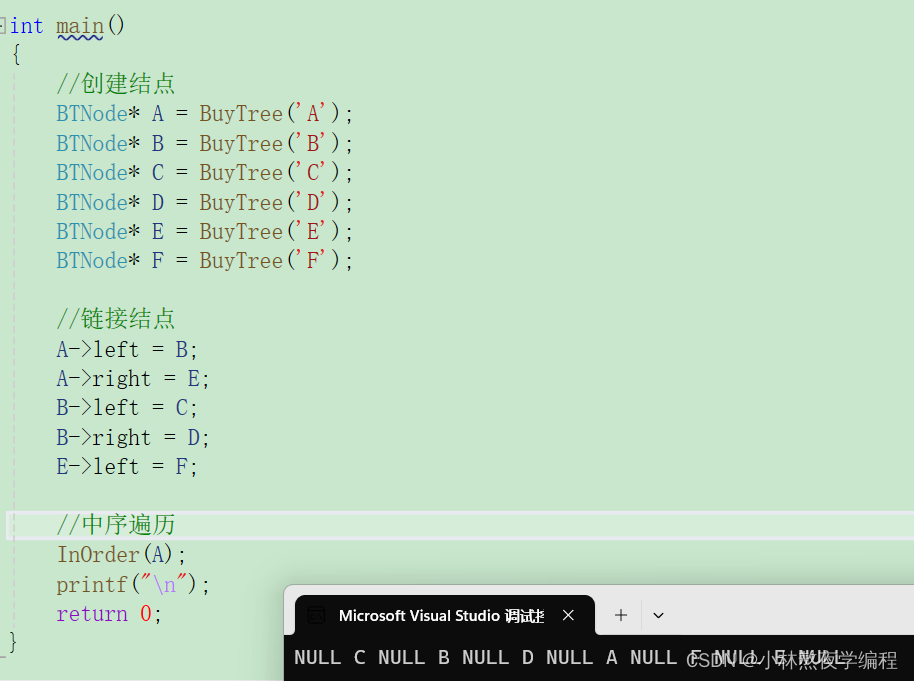
  5、后序遍历

  后序遍历，又称后根遍历。

  遍历顺序：左子树，右子树，根。

  代码实现

  void PostOrder(BTNode* root)
  {
  	if (root == NULL)
  	{
  		printf("NULL ");
  		return;
  	}
  	PostOrder(root->left);//左子树
  	PostOrder(root->right);//右子树
  	printf("%c ", root->data);//根
  }
  

  测试

  

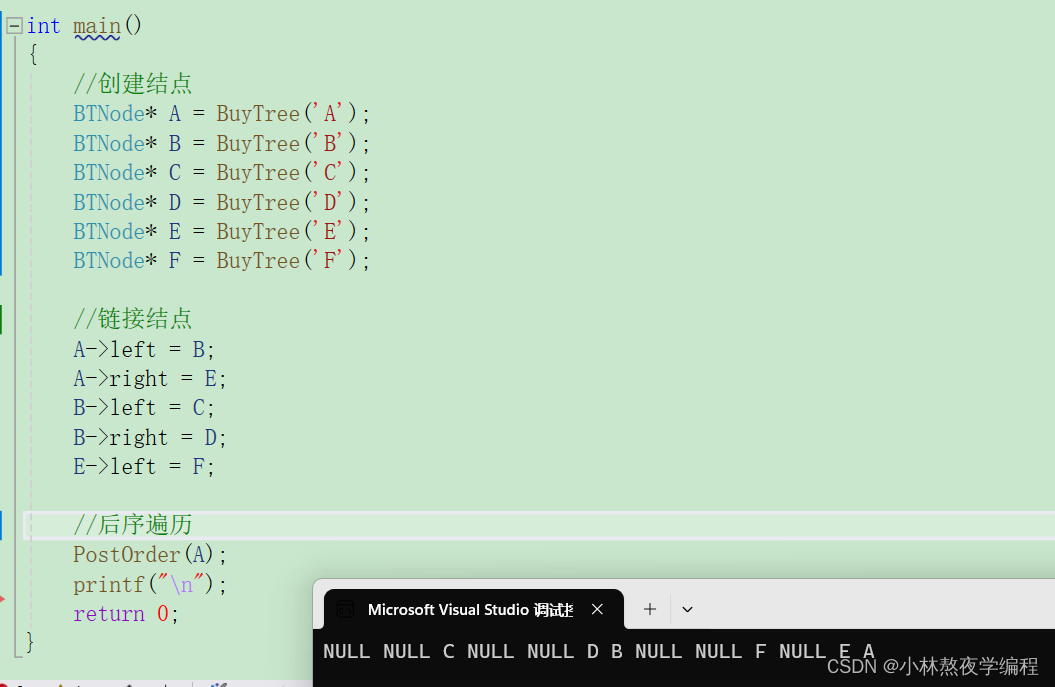
  6、层序遍历

  层序遍历，自上到下，自左到右依次访问数的结点就是层序遍历。

  思想（借助一个队列）：

  1、先将根节点入队，然后开始从队头出数据

  2、出队头的数据同时将队头左右子树的结点入队（遇到NULL则不入队）

  3、重复第二步，直到队列为空

  

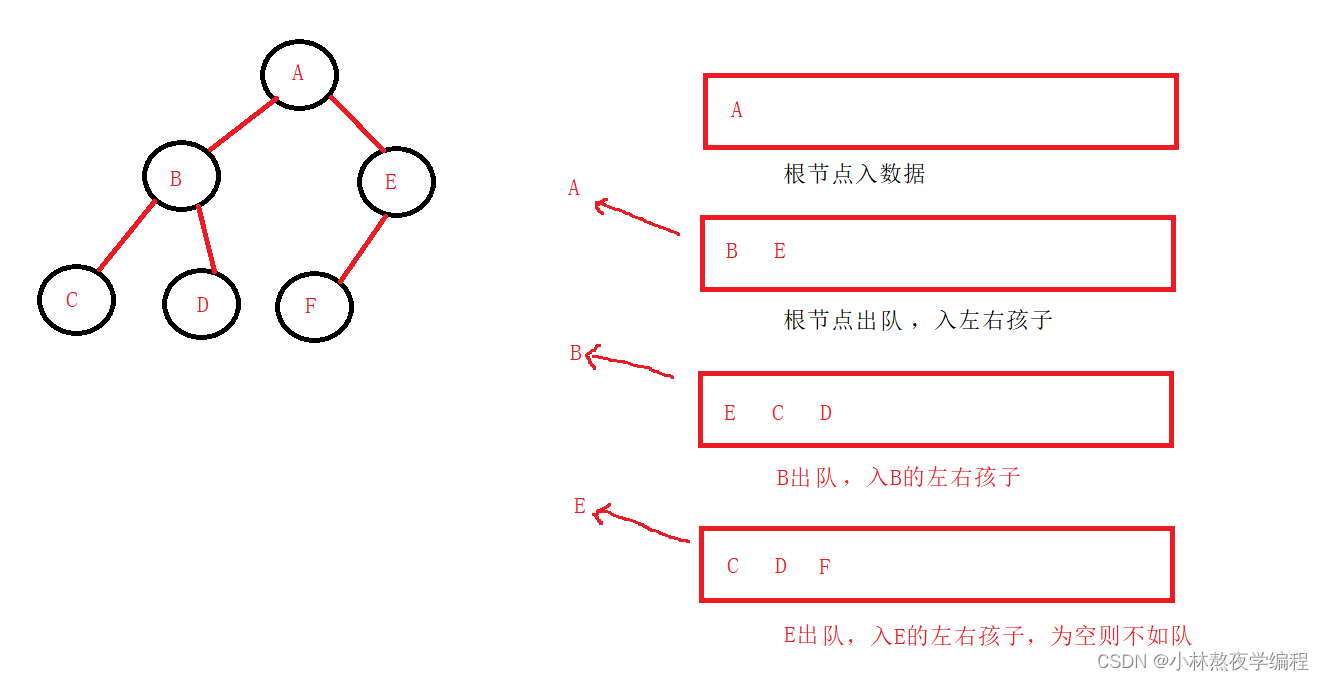
  代码实现

  void LevelOrder(BTNode* root)
  {
  	Queue q;//创建爱你队列
  	QueueInit(&q);//初始化队列
  	if (root)//根节点不为空则入队
  		QueuePush(&q, root);
  	while (!QueueEmpty(&q))//队列不为空，循环继续
  	{
  		BTNode* front = QueueFront(&q);
  		QueuePop(&q);//出队
  		printf("%c ", front->data);//打印数据
  		if (front->left)//如果左子树不为空则入队
  			QueuePush(&q, front->left);
  		if (front->right)//右子树不为空入队
  			QueuePush(&q, front->right);
  	}
  	QueueDestory(&q);//销毁队列
  }
  

  测试

  

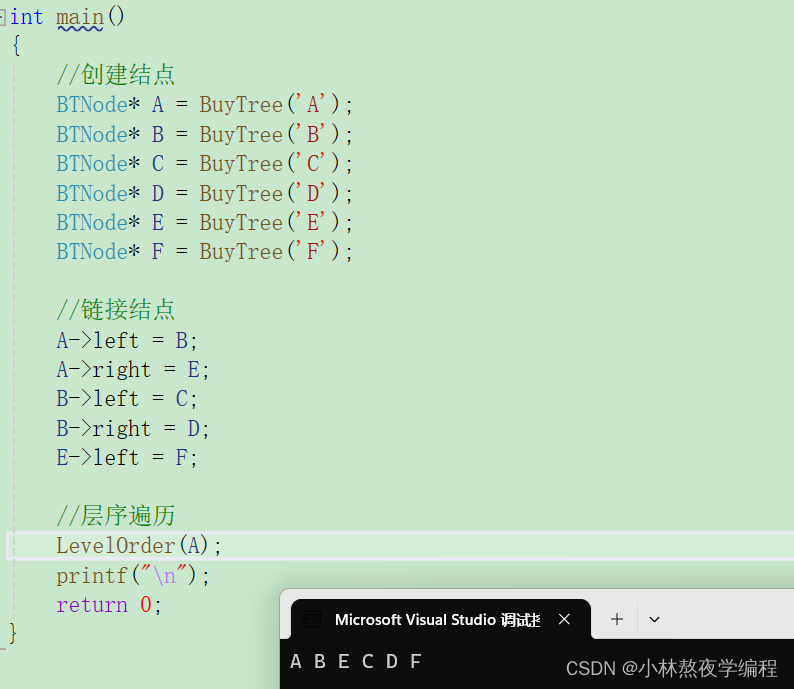
  7、计算结点个数

  计算结点个数时，可以将问题拆成子问题

  1、为空时，结点个数为0

  2、不为空时，结点个数=左子树结点个数+右子树结点个数+1(根节点)

  代码实现

  int TreeSize(BTNode* root)
  {
  	return root==NULL?0:TreeSize(root->left) + TreeSize(root->right) + 1;
  }
  

  测试

  

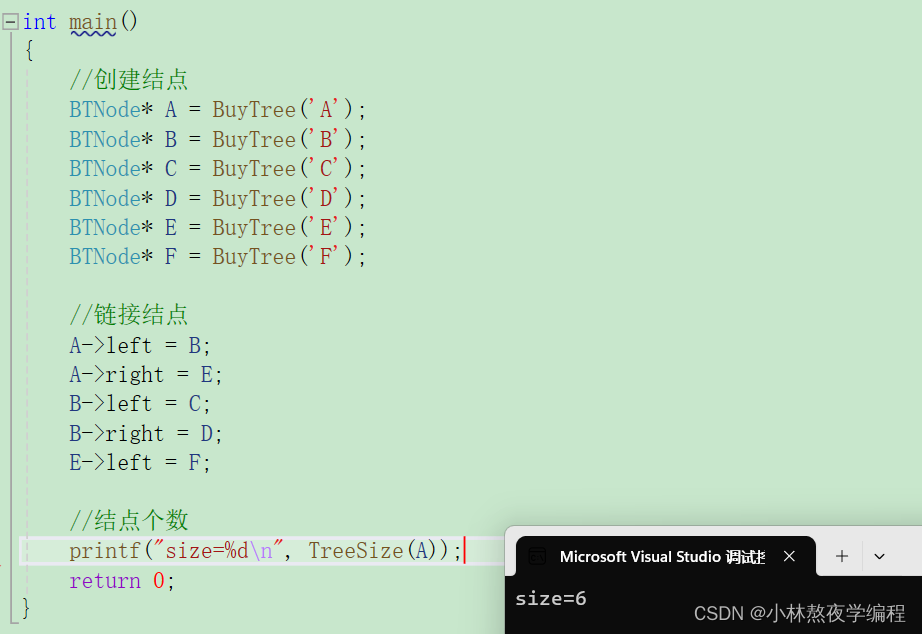
  8、计算叶子结点个数

  计算叶子结点个数时，可以将问题拆成子问题

  1、为空时，叶子结点个数为0

  2、结点左右孩子为空时，叶子结点个数为1

  3、结点不为空，叶子结点个数=左子树叶子结点个数+右子树叶子结点个数

  代码实现

  int TreeLeafSize(BTNode* root)
  {
  	if (root == NULL)
  	{
  		return 0;
  	}
  	if (root->left == NULL && root->right==NULL)
  	{
  		return 1;
  	}
  	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
  }
  

  测试

  

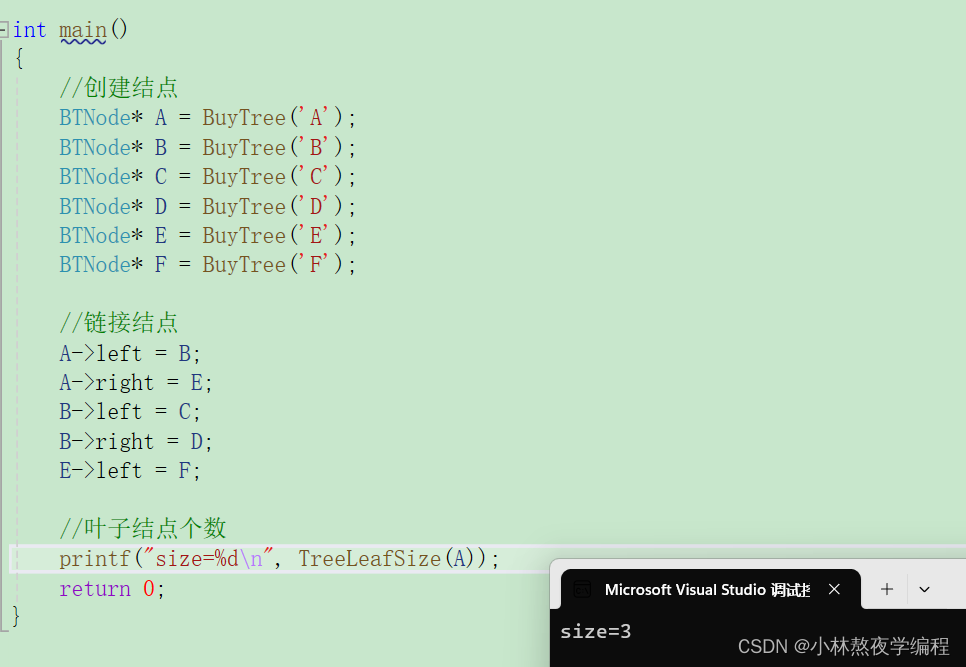
  9、计算第K层结点个数

  计算第K层结点个数时，可以将问题拆分成子问题。

  1、为空和非法时，结点个数为0个

  2、为第一层时，结点个数为1个

  3、不为空且合法时，第K层的结点个数=第K-1层的左子树结点个数+第K-1层的右子树结点个数

  代码实现

  //第k层结点的个数
  int TreeKLevelSize(BTNode* root, int k)
  {
  	if (k < 1 || root == NULL)//空树或输入k值不合法
  		return 0;
  	if (k == 1)//第一层结点个数
  		return 1;
    //不为空且合法时，第K层的结点个数=第K-1层的左子树结点个数+第K-1层的右子树结点个数
  	return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
  }
  

  测试

  

  10、计算树的最大深度

  计算树的最大深度时，可以将问题拆成子问题

  1、为空时，深度为0

  2、不为空时，最大深度为左子树和右子树较大的深度+1(自己)

  代码实现

  int maxDepth(BTNode* root) {
  	if (root == NULL)
  		return 0;//为空，深度为0
  	int leftDepth = maxDepth(root->left);//记录左子树最大深度
  	int rightDepth = maxDepth(root->right);//记录右子树最大深度
      //不为空时，最大深度为左子树和右子树较大的深度+1(自己)
  	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
  }
  

  测试

  

  总结

  本篇博客就结束啦，谢谢大家的观看，如果公主少年们有好的建议可以留言喔，谢谢大家啦！