14- OpenCV：像素重映射和直方图相关处理

目录

一、像素重映射

1、像素重映射的含义

2、应用场景

3、相关的API（例子演示）

二、直方图

1、直方图的介绍

2、直方图均衡化

3、直方图计算（归一化）

4、直方图比较

5、直方图反向投影

---

一、像素重映射

1、像素重映射的含义

        像素重映射（Pixel Remapping）是一种图像处理技术，用于将图像从一个坐标系统映射到另一个坐标系统。它通常用于校正图像中的几何畸变或调整图像的大小和分辨率。

        在像素重映射中，每个像素的位置会被重新计算，并在新的位置上进行插值或填充操作，以生成重映射后的图像。这涉及到对原始图像的坐标变换、采样和插值等处理步骤。

        简单点说：就是把输入图像中各个像素按照一定的规则映射到另外一张图像的对应位置上去，形成一张新的图像。

对称映射：（镜像效果）

2、应用场景

（1）几何校正：当相机或成像设备存在透视畸变或镜头畸变时，可以使用像素重映射来校正图像中的几何形状，使其更符合实际场景。

（2）图像缩放：通过像素重映射，可以将图像的大小调整为所需的尺寸。例如，将高分辨率图像缩小为低分辨率图像，或将低分辨率图像放大为高分辨率图像。

（3）图像扭曲：通过像素重映射，可以对图像进行扭曲或形变，以实现特定的效果。例如，可以将图像进行弯曲、拉伸或旋转，用于艺术创作或特殊效果。

（4）图像拼接：在图像拼接或全景图像生成中，像素重映射可以用于将多个图像的坐标系统对齐，并进行像素级别的融合，以生成无缝连接的全景图像。

需要注意的是，像素重映射可能会引入一定程度的信息损失或伪影，特别是在图像放大或形变较大的情况下。因此，在实际应用中，需要根据具体需求和图像特性来选择合适的像素重映射算法和参数设置。

3、相关的API（例子演示）

（1）cv::remap

remap(

InputArray src,// 输入图像

OutputArray dst,// 输出图像

InputArray  map1,// x 映射表 CV_32FC1/CV_32FC2

InputArray map2,// y 映射表

int interpolation,// 选择的插值方法，常见线性插值，可选择立方等

int borderMode,// BORDER_CONSTANT

const Scalar borderValue// color

)

（2）代码演示：

该示例，有四种重映射的方式（缩小，左右镜像，上下镜像，上下、左右都进行镜像），可以通过输入的按键数字来不断变化。

#include 
#include 
#include 
using namespace cv;
Mat src, dst, map_x, map_y;
const char* OUTPUT_TITLE = "remap demo";
int index = 0;
void update_map(void);
int main(int argc, char** argv) {
	src = imread("test.jpg");
	if (!src.data) {
		printf("could not load image...\n");
		return -1;
	}
	char input_win[] = "input image";
	namedWindow(input_win, CV_WINDOW_AUTOSIZE);
	namedWindow(OUTPUT_TITLE, CV_WINDOW_AUTOSIZE);
	imshow(input_win, src);
	map_x.create(src.size(), CV_32FC1);
	map_y.create(src.size(), CV_32FC1);
	int c = 0;
	while (true) {
		c = waitKey(500);
		if ((char)c == 27) {
			break;
		}
		index = c % 4;
		update_map();
		remap(src, dst, map_x, map_y, INTER_LINEAR, BORDER_CONSTANT, Scalar(0, 255, 255));
		imshow(OUTPUT_TITLE, dst);
	}
	return 0;
}
void update_map(void) {
	for (int row = 0; row < src.rows; row++) {
		for (int col = 0; col < src.cols; col++) {
			switch (index) {
			case 0: //缩小一半
				if (col > (src.cols * 0.25) && col <= (src.cols*0.75) && row > (src.rows*0.25) && row <= (src.rows*0.75)) {
                    // -0.5主要是因为边缘有黄色的线，去掉
					map_x.at(row, col) = 2 * (col - (src.cols*0.25) -0.5);
					map_y.at(row, col) = 2 * (row - (src.rows*0.25) -0.5);
				}
				else {
					map_x.at(row, col) = 0;
					map_y.at(row, col) = 0;
				}
				break;
			case 1: // XF方向的对调
				map_x.at(row, col) = (src.cols - col - 1);
				map_y.at(row, col) = row;
				break;
			case 2: // Y方向的对调
				map_x.at(row, col) = col;
				map_y.at(row, col) = (src.rows - row - 1);
				break;
			case 3: // XY方向同时对调
				map_x.at(row, col) = (src.cols - col - 1);
				map_y.at(row, col) = (src.rows - row - 1);
				break;
			}
		}
	}
}

二、直方图

1、直方图的介绍

（1）直方图的含义

直方图是一种用于可视化数据分布的图形表示方法。它将数据按照不同数值范围进行分组，并统计每个数值范围内的数据频次或频率。直方图可以帮助我们了解数据的分布情况、集中程度和偏斜程度。

图像直方图，是指对整个图像像在灰度范围内的像素值(0~255)统计出现频率次数，据此生成的直方图，称为图像直方图-直方图。直方图反映了图像灰度的分布情况。是图像的统计学特征。

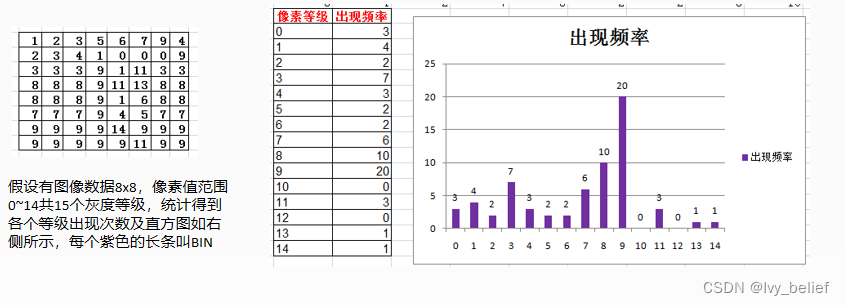
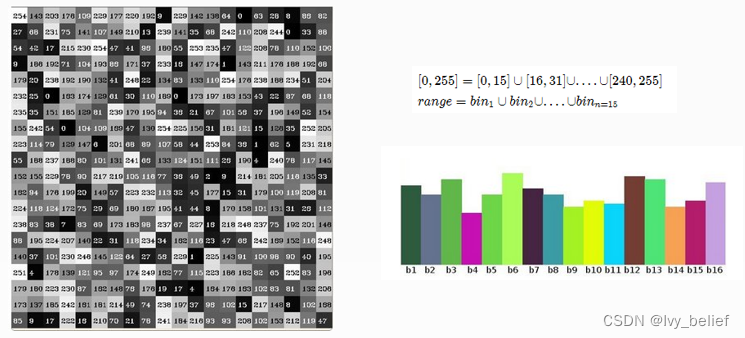
总结：上述直方图概念是基于图像像素值，其实对图像梯度、每个像素的角度、等一切图像的属性值，我们都可以建立直方图。这个才是直方图的概念真正意义，不过是基于图像像素灰度直方图是最常见的。

（2）直方图的属性（常见）

- dims 表示维度，对灰度图像来说只有一个通道值dims=1  

- bins 表示在维度中子区域大小划分，bins=256，划分为256个级别  

- range 表示值得范围，灰度值范围为[0~255]之间  

2、直方图均衡化

（1）直方图均衡化（Histogram Equalization）是一种用于增强图像对比度的图像处理技术。

        它通过重新分配图像像素的灰度级，使得图像的直方图在整个灰度范围内更加均匀分布，从而提高图像的视觉效果和可识别性。

直方图均衡化是一种提高图像对比度的方法，拉伸图像灰度值范围。

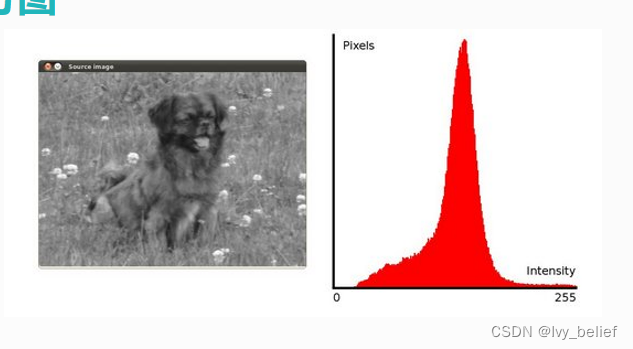
将直方图集中的地方就进行拉伸。

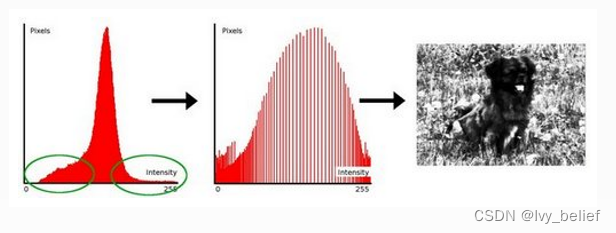
（2）直方图均衡化过程：

        1）计算原始图像的灰度直方图：统计原始图像中每个灰度级的像素数量。

        2）计算累积分布函数（CDF）：将灰度直方图进行归一化，并计算每个灰度级的累积概率。

        3）映射原始图像的灰度级：根据CDF，将原始图像中的每个像素的灰度级映射到新的灰度级上。映射规则可以使用线性插值或其他非线性函数来实现。

        4）生成均衡化后的图像：将映射后的灰度级应用于原始图像的每个像素，生成均衡化后的图像。

直方图均衡化可以有效地扩展图像的动态范围，使得图像中的细节更加清晰可见。它特别适用于那些具有较窄灰度范围的图像，如低对比度图像或受光照不均匀影响的图像。

需要注意的是，直方图均衡化可能会增加图像中噪声的可见性，并且在某些情况下可能导致图像过度增强或失真。因此，在应用直方图均衡化时，需要根据具体情况进行调整和优化，以达到最佳的效果。

简单来说：如何实现，通过上一课中的remap我们知道可以将图像灰度分布从一个分布映射到另外一个分布，然后在得到映射后的像素值即可。

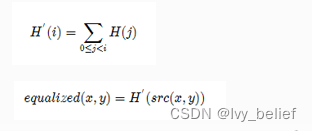
（3）cv::equalizeHist

equalizeHist(

InputArray src,//输入图像，必须是8-bit的单通道图像

OutputArray dst// 输出结果 )

（4）关键实现的代码示例

Mat src, dst;
// 加载图像
src = imread("D:/vcprojects/images/test.png");
// 转化为灰度图像
cvtColor(src, src, CV_BGR2GRAY)；
// 直方图均衡化
equalizeHist(src, dst);

3、直方图计算（归一化）

（1）含义：直方图的计算是指对一组数据进行统计和分组，然后根据数据的取值范围将其分配到不同的区间，并统计每个区间内数据的频次或频率。

（2）直方图的计算步骤：

        1）确定数据的取值范围：首先需要确定数据的最小值和最大值，以便确定直方图的横轴范围。

        2）分组：根据数据的取值范围，将整个范围划分为若干个等宽的区间（也称为箱子或柱），每个区间代表一个数据范围。

        3）统计频次或频率：遍历数据集，将每个数据按照其取值分配到对应的区间中，并记录该区间内数据的频次（出现次数）或频率（出现次数与总数的比例）。

        4）绘制直方图：根据统计得到的频次或频率，绘制直方图。通常，直方图的横轴表示数据的取值范围，纵轴表示对应范围内的数据频次或频率。每个柱状条代表一个区间，其高度表示该区间内数据的频次或频率。

        直方图的计算可以帮助我们了解数据的分布情况，例如数据的集中程度、偏斜程度和离群值等。通过观察直方图，我们可以获得对数据特征的直观认识，并进一步进行数据分析和决策。

（3）cv::split 和 cv::calcHist

//把多通道图像分为多个单通道图像

split(

const Mat &src, //输入多通道的图像

Mat* mvbegin // 输出的单通道图像数组

）

// 直方图计算

calcHist(

const Mat* images,//输入图像指针

int images,// 图像数目

const int* channels,// 通道数

InputArray mask,// 输入mask，可选，不用

OutputArray hist,//输出的直方图数据

int dims,// 维数，就取一维

const int* histsize,// 直方图级数

const float* ranges,// 值域范围

bool uniform,// true by default

bool accumulate// false by defaut

)

（4）代码演示：

了解下：归一化

归一化（Normalization）是一种常用的数据预处理技术，用于将不同取值范围的数据转换为统一的标准范围，以便更好地进行比较和分析。在机器学习中，归一化通常是指将特征数据缩放到一个特定的范围，以消除特征之间的量纲差异。

// 函数原型

void cv::normalize(

InputArray src, // 输入数组，即需要进行归一化的数据。

OutputArray dst, // 输出数组，即归一化后的结果。

double alpha = 1.0, // 归一化范围的缩放因子。

double beta = 0.0, // 归一化范围的平移因子。

int norm_type = NORM_L2, // 归一化类型，可选值包括NORM_INF、NORM_L1、NORM_L2和NORM_MINMAX等，默认为NORM_L2。

int dtype = -1, // 输出数组的数据类型，如果为负数，则使用输入数组的数据类型。

InputArray mask = noArray() // 可选的掩码数组，用于指定要处理的元素。

);

通过调用normalize函数，可以将输入数组src进行归一化操作，并将结果存储在输出数组dst中。归一化范围由alpha和beta参数确定，具体的归一化方式由norm_type参数指定。

需要注意的是，normalize函数可以用于对图像、矩阵等多种数据类型进行归一化操作，并且可以根据实际需求选择不同的归一化方式和参数。

#include 
#include 
#include 
using namespace std;
using namespace cv;
int main(int argc, char** argv) {
	Mat src = imread("cat.png");
	if (!src.data) {
		printf("could not load image...\n");
		return -1;
	}
	char INPUT_T[] = "input image";
	char OUTPUT_T[] = "histogram demo";
	namedWindow(INPUT_T, CV_WINDOW_AUTOSIZE);
	namedWindow(OUTPUT_T, CV_WINDOW_AUTOSIZE);
	imshow(INPUT_T, src);
	// 分通道显示
	vector bgr_planes;
	split(src, bgr_planes);
	//imshow("single channel demo", bgr_planes[0]);
	// 计算直方图
	int histSize = 256;
	float range[] = { 0, 256 };
	const float *histRanges = { range };
	Mat b_hist, g_hist, r_hist;
	calcHist(&bgr_planes[0], 1, 0, Mat(), b_hist, 1, &histSize, &histRanges, true, false);
	calcHist(&bgr_planes[1], 1, 0, Mat(), g_hist, 1, &histSize, &histRanges, true, false);
	calcHist(&bgr_planes[2], 1, 0, Mat(), r_hist, 1, &histSize, &histRanges, true, false);
	// 归一化
	int hist_h = 400;
	int hist_w = 512;
	int bin_w = hist_w / histSize;
	Mat histImage(hist_w, hist_h, CV_8UC3, Scalar(0, 0, 0));
	normalize(b_hist, b_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
	normalize(g_hist, g_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
	normalize(r_hist, r_hist, 0, hist_h, NORM_MINMAX, -1, Mat());
	// render histogram chart
	for (int i = 1; i < histSize; i++) {
		line(histImage, Point((i - 1)*bin_w, hist_h - cvRound(b_hist.at(i - 1))), 
			Point((i)*bin_w, hist_h - cvRound(b_hist.at(i))), Scalar(255, 0, 0), 2, LINE_AA);
		line(histImage, Point((i - 1)*bin_w, hist_h - cvRound(g_hist.at(i - 1))),
			Point((i)*bin_w, hist_h - cvRound(g_hist.at(i))), Scalar(0, 255, 0), 2, LINE_AA);
		line(histImage, Point((i - 1)*bin_w, hist_h - cvRound(r_hist.at(i - 1))),
			Point((i)*bin_w, hist_h - cvRound(r_hist.at(i))), Scalar(0, 0, 255), 2, LINE_AA);
	}
	imshow(OUTPUT_T, histImage);
	waitKey(0);
	return 0;
}

效果展示：

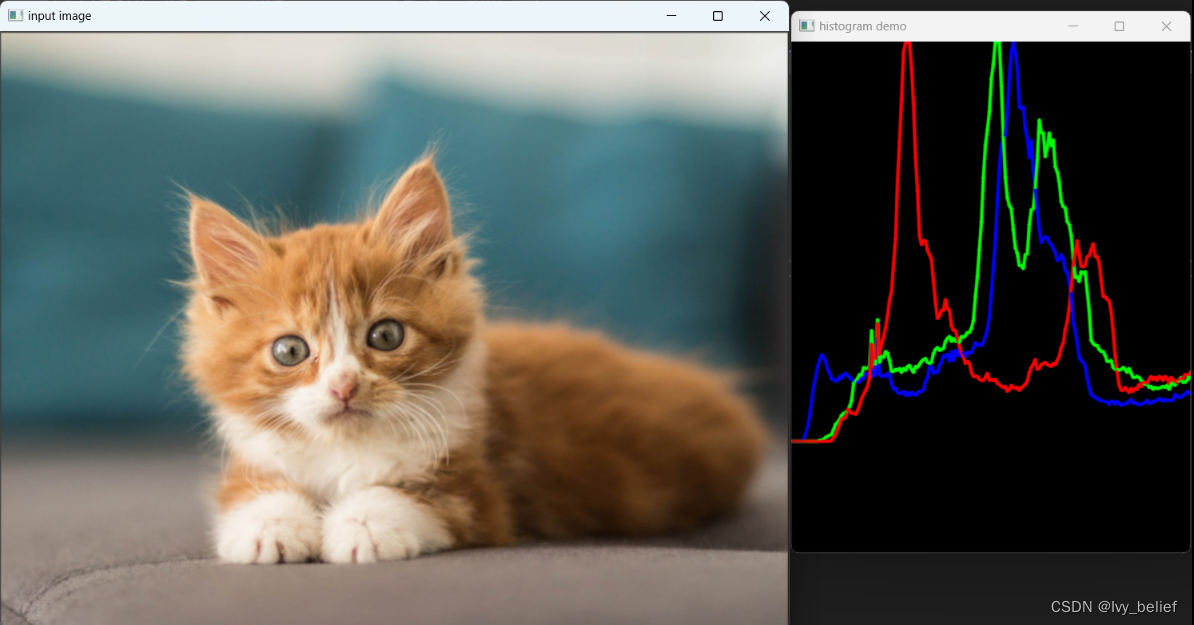
4、直方图比较

（1）含义：对输入的两张图像计算得到直方图H1与H2，归一化到相同的尺度空间 然后可以通过计算H1与H2的之间的距离得到两个直方图的相似程度进 而比较图像本身的相似程度。

（2）直方图比较的四种方法：

Correlation 相关性比较

Chi-Square 卡方比较

Intersection 十字交叉性

Bhattacharyya distance 巴氏距离

        1）直方图比较方法-相关性计算(CV_COMP_CORREL)

        2）直方图比较方法-卡方计算(CV_COMP_CHISQR)

        H1,H2分别表示两个图像的直方图数据

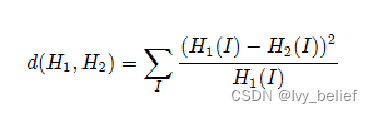
        3）直方图比较方法-十字计算(CV_COMP_INTERSECT)

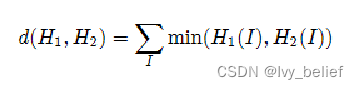
        4）直方图比较方法-巴氏距离计算(CV_COMP_BHATTACHARYYA )

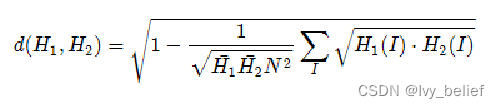
（3）直方图比较的步骤：

- 首先把图像从RGB色彩空间转换到HSV色彩空间cvtColor

- 计算图像的直方图，然后归一化到[0~1]之间calcHist和normalize;

- 使用上述四种比较方法之一进行比较compareHist

（4）cv::compareHist

compareHist(

InputArray h1, // 直方图数据，下同

InputArray H2,

int method// 比较方法，上述四种方法之一

)

（5）代码演示：

#include 
#include 
#include 
using namespace std;
using namespace cv;
string convertToString(double d);
int main(int argc, char** argv) {
	Mat base, test1, test2;
	Mat hsvbase, hsvtest1, hsvtest2;
	base = imread("test.jpg");
	if (!base.data) {
		printf("could not load image...\n");
		return -1;
	}
	test1 = imread("cat.png");
	test2 = imread("catnoise.png");
	cvtColor(base, hsvbase, CV_BGR2HSV);
	cvtColor(test1, hsvtest1, CV_BGR2HSV);
	cvtColor(test2, hsvtest2, CV_BGR2HSV);
	int h_bins = 50; int s_bins = 60;     
	int histSize[] = { h_bins, s_bins };
	// hue varies from 0 to 179, saturation from 0 to 255     
	float h_ranges[] = { 0, 180 };     
	float s_ranges[] = { 0, 256 };
	const float* ranges[] = { h_ranges, s_ranges };
	// Use the o-th and 1-st channels     
	int channels[] = { 0, 1 };
	MatND hist_base;
	MatND hist_test1;
	MatND hist_test2;
	calcHist(&hsvbase, 1,  channels, Mat(), hist_base, 2, histSize, ranges, true, false);
	normalize(hist_base, hist_base, 0, 1, NORM_MINMAX, -1, Mat());
	calcHist(&hsvtest1, 1, channels, Mat(), hist_test1, 2, histSize, ranges, true, false);
	normalize(hist_test1, hist_test1, 0, 1, NORM_MINMAX, -1, Mat());
	calcHist(&hsvtest2, 1, channels, Mat(), hist_test2, 2, histSize, ranges, true, false);
	normalize(hist_test2, hist_test2, 0, 1, NORM_MINMAX, -1, Mat());
	
	double basebase = compareHist(hist_base, hist_base, CV_COMP_INTERSECT);
	double basetest1 = compareHist(hist_base, hist_test1, CV_COMP_INTERSECT);
	double basetest2 = compareHist(hist_base, hist_test2, CV_COMP_INTERSECT);
	double tes1test2 = compareHist(hist_test1, hist_test2, CV_COMP_INTERSECT);
	printf("test1 compare with test2 correlation value :%f", tes1test2);
	Mat test12;
	test2.copyTo(test12);
	putText(base, convertToString(basebase), Point(50, 50), CV_FONT_HERSHEY_COMPLEX, 1, Scalar(0, 0, 255), 2, LINE_AA);
	putText(test1, convertToString(basetest1), Point(50, 50), CV_FONT_HERSHEY_COMPLEX, 1, Scalar(0, 0, 255), 2, LINE_AA);
	putText(test2, convertToString(basetest2), Point(50, 50), CV_FONT_HERSHEY_COMPLEX, 1, Scalar(0, 0, 255), 2, LINE_AA);
	putText(test12, convertToString(tes1test2), Point(50, 50), CV_FONT_HERSHEY_COMPLEX, 1, Scalar(0, 0, 255), 2, LINE_AA);
	
	namedWindow("base", CV_WINDOW_AUTOSIZE);
	namedWindow("test1", CV_WINDOW_AUTOSIZE);
	namedWindow("test2", CV_WINDOW_AUTOSIZE);
	imshow("base", base);
	imshow("test1", test1);
	imshow("test2", test2);
	imshow("test12", test12);
	waitKey(0);
	return 0;
}
string convertToString(double d) {
	ostringstream os;
	if (os << d)
		return os.str();
	return "invalid conversion";
}

5、直方图反向投影

（1）反向投影（Back Projection）

反向投影是反映直方图模型在目标图像中的分布情况

简单点说：就是用直方图模型去目标图像中寻找是否有相似的对象。通常用HSV色彩空间的HS两个通道直方图模型。

（2）反向投影的步骤

1.建立直方图模型

2.计算待测图像直方图并映射到模型中

3.从模型反向计算生成图像

步骤+相关的API

- 加载图片imread

- 将图像从RGB色彩空间转换到HSV色彩空间cvtColor

- 计算直方图和归一化calcHist与normalize

- Mat与MatND其中Mat表示二维数组，MatND表示三维或者多维数据，此处均可以用Mat表示。

-计算反向投影图像 - calcBackProject

（3）代码演示：

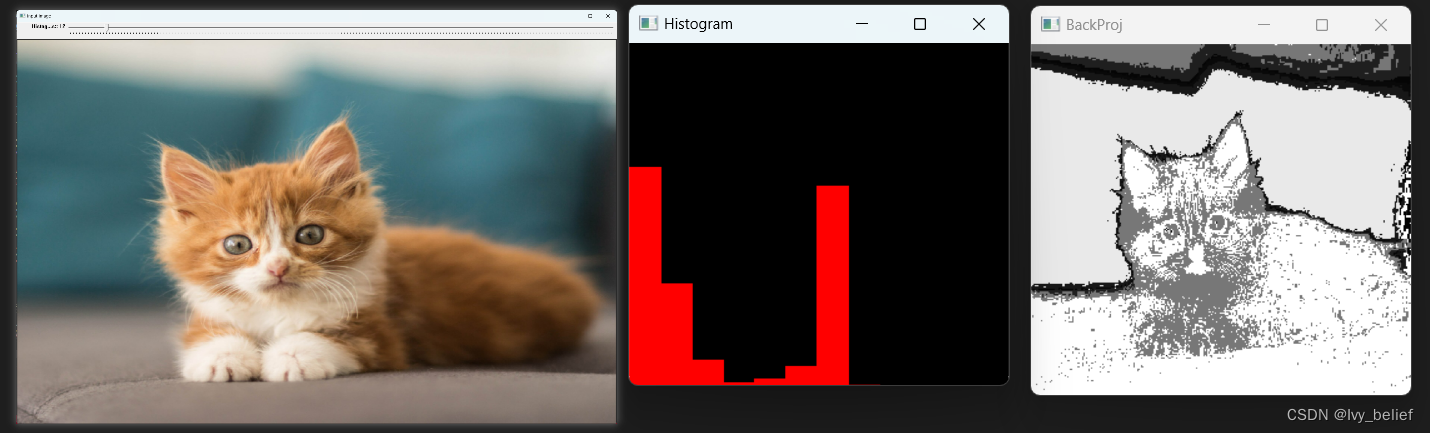
#include 
#include 
#include 
using namespace std;
using namespace cv;
Mat src; Mat hsv; Mat hue; 
int bins = 12;
void Hist_And_Backprojection(int, void*);
int main(int argc, char** argv) {
	src = imread("test.jpg");
	if (src.empty()) {
		printf("could not load image...\n");
		return -1;
	}
	const char*  window_image = "input image";
	namedWindow(window_image, CV_WINDOW_NORMAL);
	namedWindow("BackProj", CV_WINDOW_NORMAL);
	namedWindow("Histogram", CV_WINDOW_NORMAL);
	cvtColor(src, hsv, CV_BGR2HSV);
	hue.create(hsv.size(), hsv.depth());
	int nchannels[] = { 0, 0 };
	mixChannels(&hsv, 1, &hue, 1, nchannels, 1);
	createTrackbar("Histogram Bins:", window_image, &bins, 180, Hist_And_Backprojection);
	Hist_And_Backprojection(0, 0);
	imshow(window_image, src);
	waitKey(0);
	return 0;
}
void Hist_And_Backprojection(int, void*) {
	float range[] = { 0, 180 };
	const float *histRanges = { range };
	Mat h_hist;
	calcHist(&hue, 1, 0, Mat(), h_hist, 1, &bins, &histRanges, true, false);
	normalize(h_hist, h_hist, 0, 255, NORM_MINMAX, -1, Mat());
	Mat backPrjImage;
	calcBackProject(&hue, 1, 0, h_hist, backPrjImage, &histRanges, 1, true);
	imshow("BackProj", backPrjImage);
	int hist_h = 400;
	int hist_w = 400;
	Mat histImage(hist_w, hist_h, CV_8UC3, Scalar(0, 0, 0));
	int bin_w = (hist_w / bins);
	for (int i = 1; i < bins; i++) {
		rectangle(histImage, 
			Point((i - 1)*bin_w, (hist_h - cvRound(h_hist.at(i - 1) * (400 / 255)))),
			//Point(i*bin_w, (hist_h - cvRound(h_hist.at(i) * (400 / 255)))),
			Point(i*bin_w, hist_h),
			Scalar(0, 0, 255), -1);
	}
	imshow("Histogram", histImage);
	return;
}

效果展示：